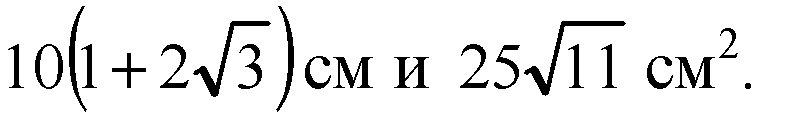Дополнительные задачи к главе I Параллельность прямых и плоскостей. → номер 102 102. Докажите, что плоскость α, проходящая через середины двух ребер основания тетраэдра и вершину, не принадлежащую основанию, параллельна третьему ребру основания. Найдите периметр и площадь сечения тетраэдра плоскостью α, если длины всех ребер тетраэдра равны 20 см.
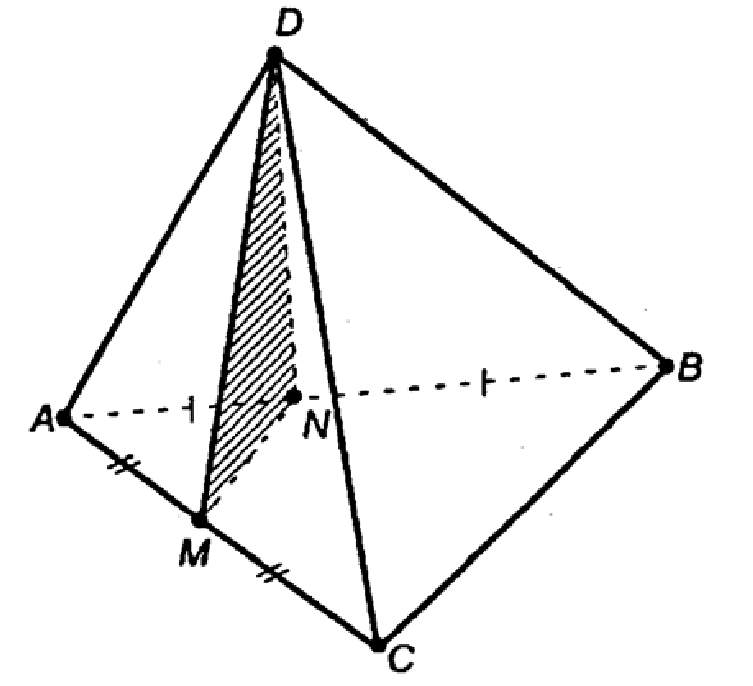
По теореме I пл. DNM || DC (MN — средняя линия ΔАВС, поэтому MN || BC).
Если все ребра тетраэдра равны, тогда в ΔADC отрезок DM — медиана, а значит и высота и биссектриса. Из ΔADM:
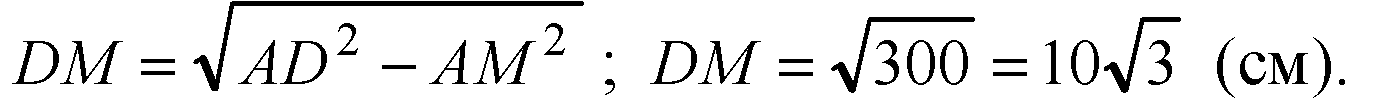
ΔAND = ΔAMD (они — прямоугольные, AD — общая гипотенуза, АМ = AN); из равенства треугольников DM= DN;
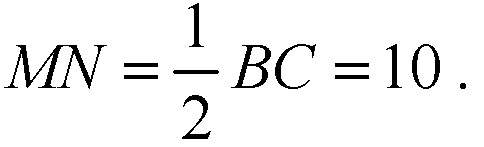
Рассмотрим ΔMDN.
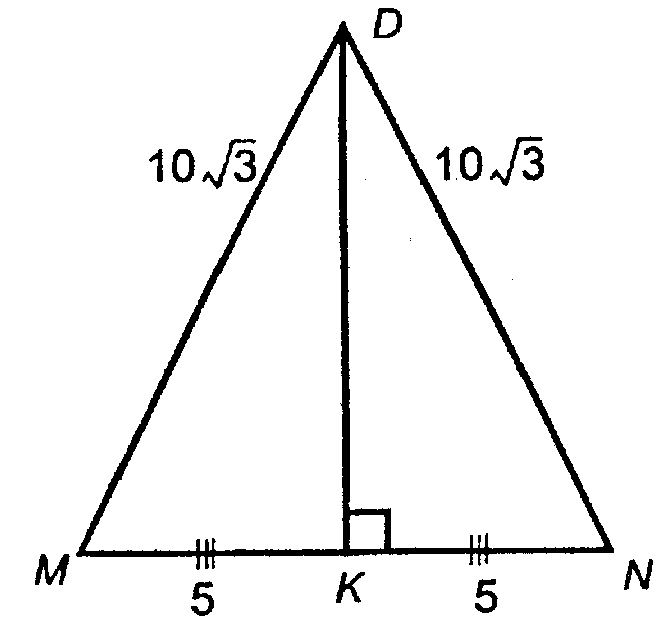
Проведем в равнобедренном ΔMDN высоту DK.
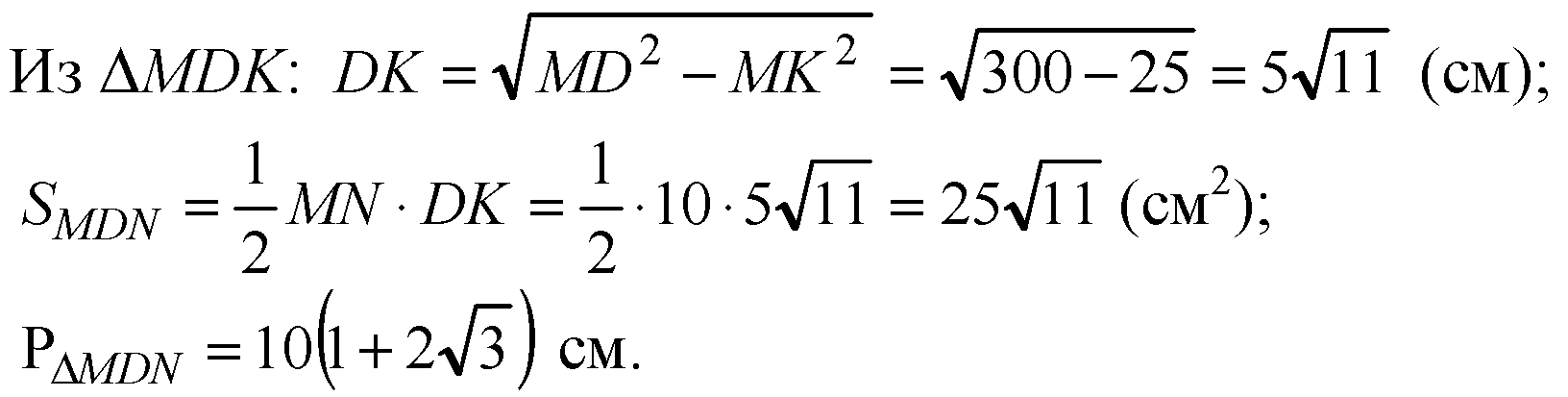
Ответ: