11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости

Введение → номер 11

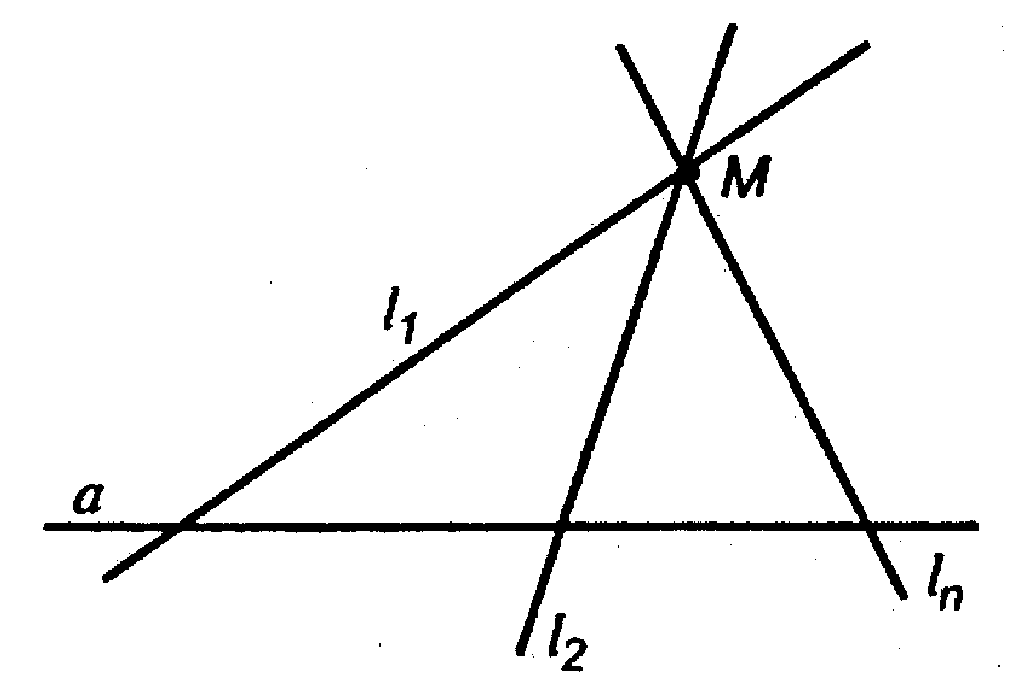
Пусть есть прямая а, точка М и М ∉ а.

Из теоремы п. 3, через а и М проходит единственная плоскость а. Прямые, пересекающие

А, пересекают ее в точке, лежащей в α. Точка М — общая для всех прямых l1, l2, l3 и М ∈ α.

Тогда по аксиоме А2 каждая прямая l1, l2, l3 лежит в плоскость α, так как две точки каждой прямой лежат в α.