112. Докажите, что сумма квадратов четырех диагоналей параллелепипеда равна сумме квадратов двенадцати его ребер

Дополнительные задачи к главе I Параллельность прямых и плоскостей. → номер 112

Будем исходить из того, что диагональное сечение параллелепипеда — параллелограмм.

Решим вспомогательную задачу: установим зависимость между сторонами параллелограмма и его диагоналями.

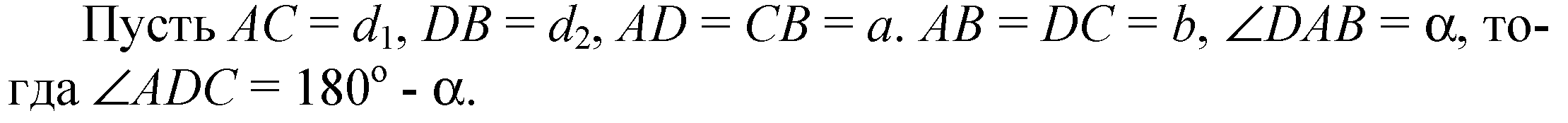
Для A DAB запишем теорему косинусов:

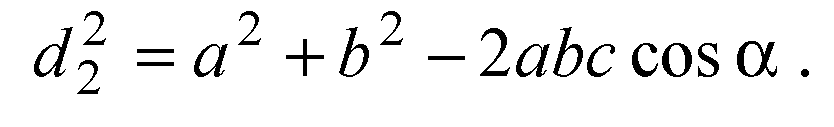
Для ΔADC запишем теорему косинусов:

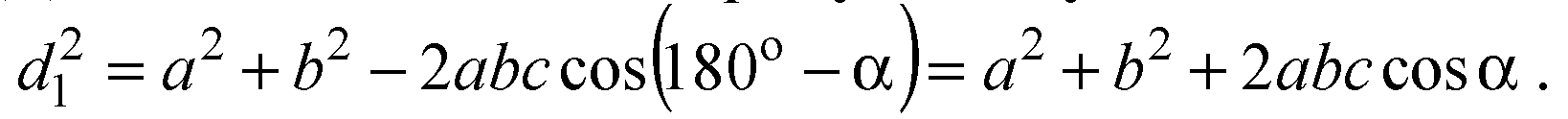
Складывая эти равенства, получаем:

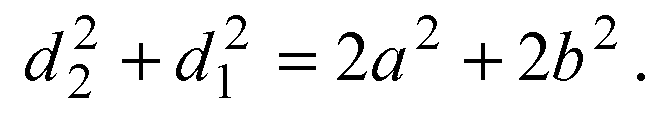
Пусть ребра параллелепипеда равны a, b, c.

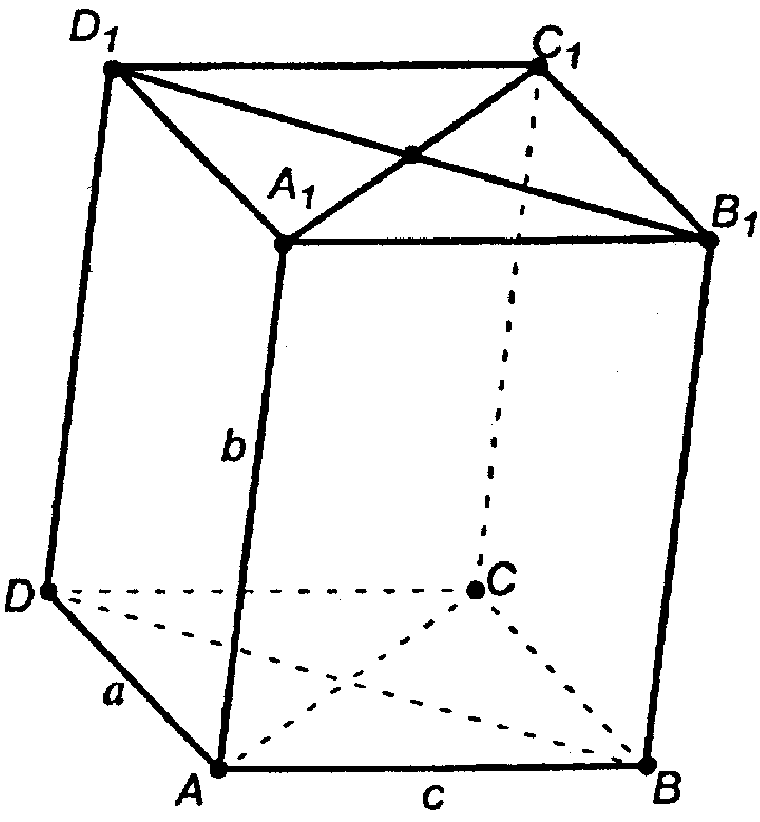
Для плоскости DD1B1B

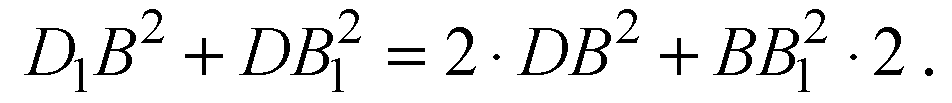
Для плоскости АА1С1С

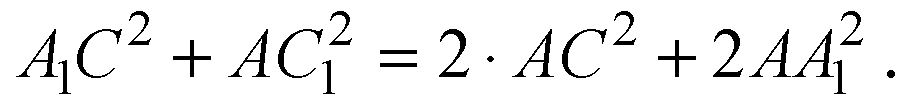
Сложим равенства:

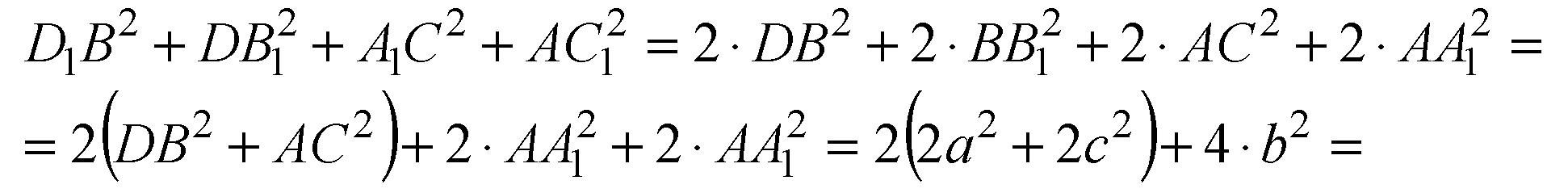
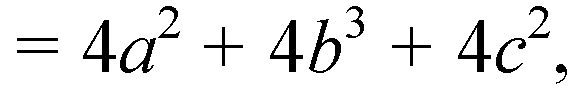
А это сумма квадратов всех ребер параллелепипеда.

Что и требовалось доказать.