Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости → номер 132
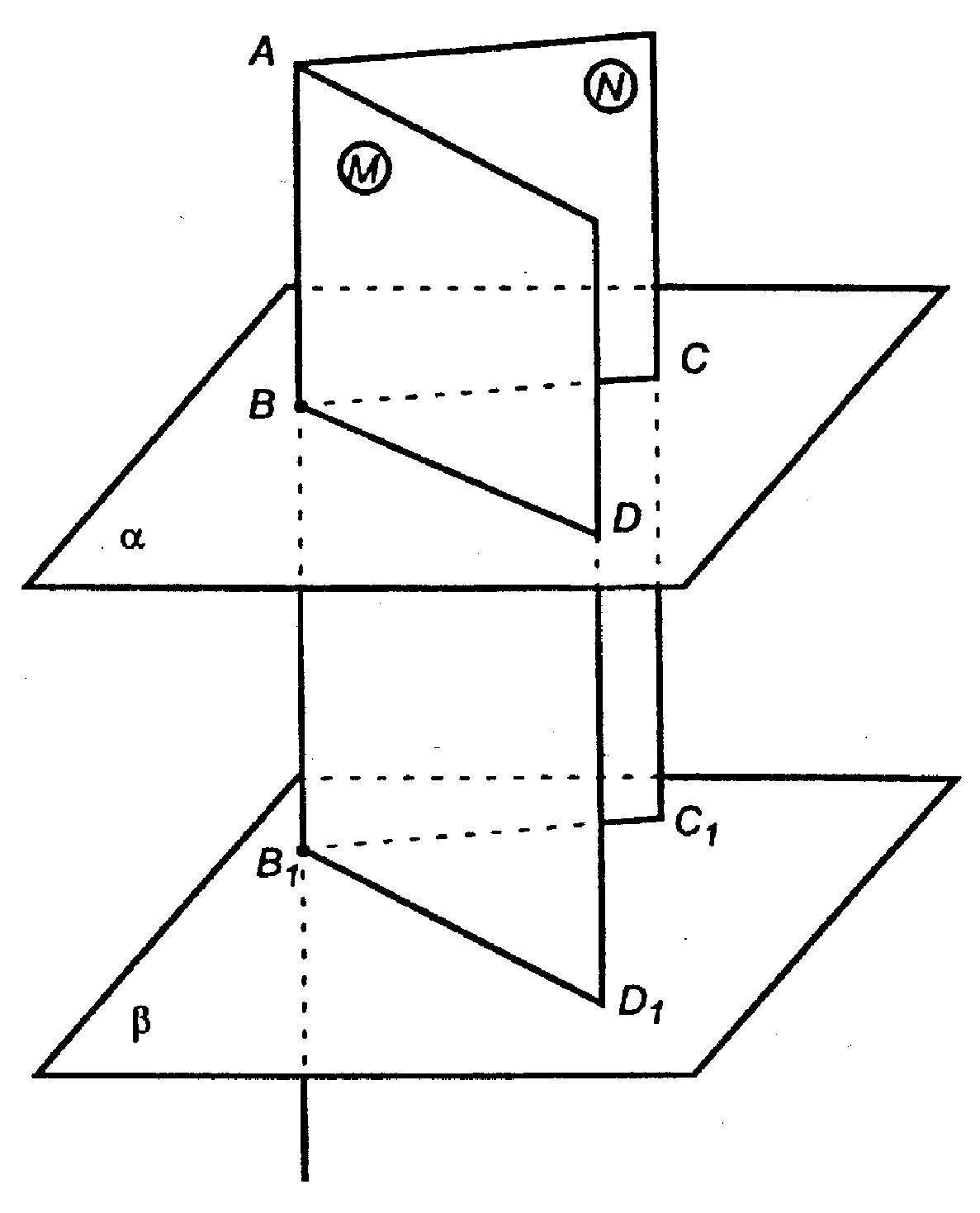
Решение:
Пусть α || β, а прямая ВВ1 ⊥ α. Докажем, что ВВ1 ⊥ β. Проведем через ВВ1 плоскости M и N;
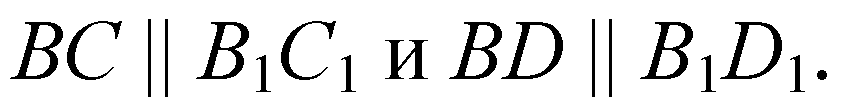
По условию ВВ1 ⊥ ВС и ВВ1 ⊥ BD (т. к. ВВ1 ⊥ α).
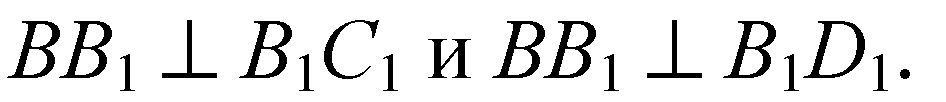
ВВ1 ⊥ β, т. к. В1С1 и ВD1 пересекаются и лежат в плоскости β.
