130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВ = n. Найдите расстояния от точки М до: а) вершин квадрата; б) прямых АС и BD

Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости → номер 130

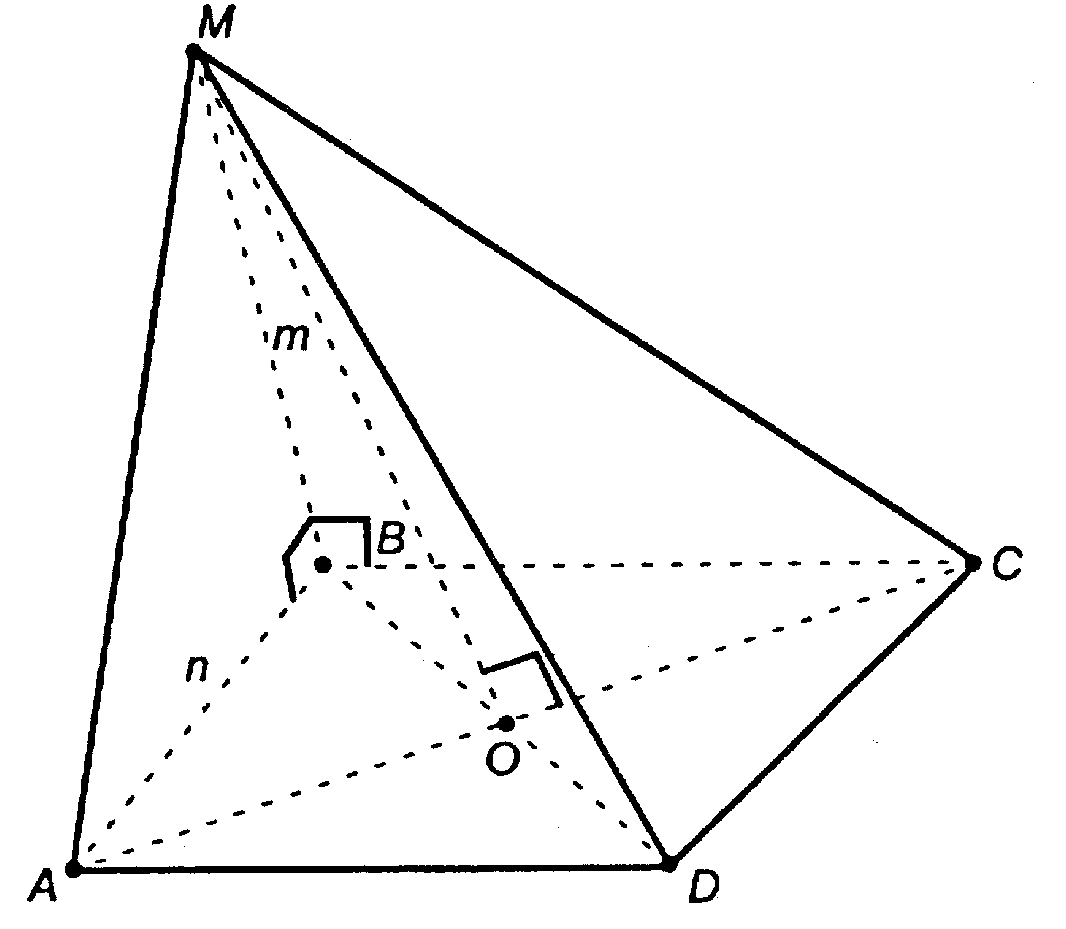
Дано:

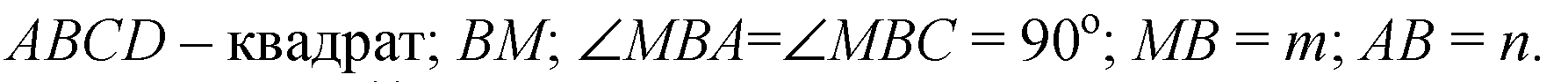
Решение

А) 1) ΔМВА = ΔМВС по условию, МВ — общий; ВА = ВС есть стороны квадрата.

Значит,

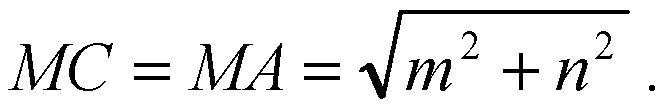
2) ΔMBD является прямоугольным, т. к. МВ ⊥ пл. АВС и BD ⊂ пл. АВС.

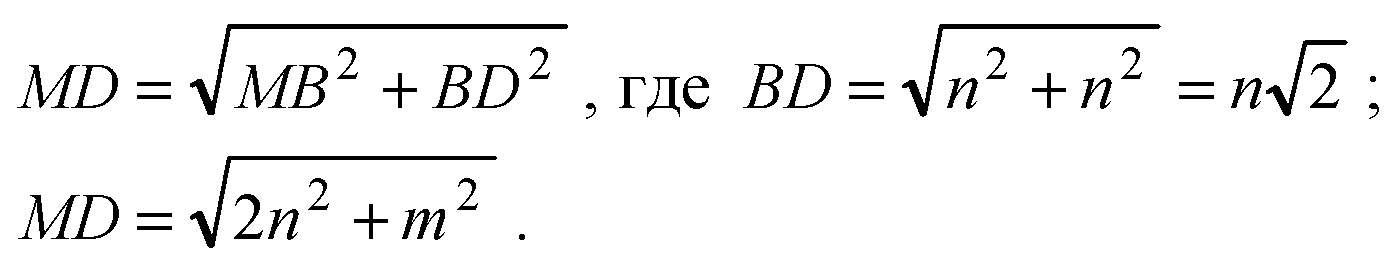
Б) По определению перпендикуляра:

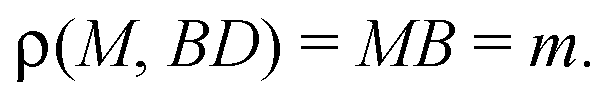
Рассмотрим ΔМВО и прямую АС.

По свойству диагоналей квадрата ВО ⊥ АС; МВ ⊥ АС, т. к. МВ ⊥ АВС; МВ не перпендикулярна ВО, тогда АС ⊥ МВО.

Значит,

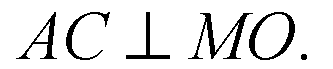
Тогда

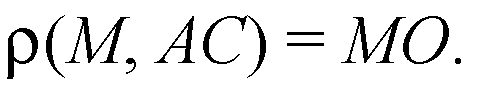
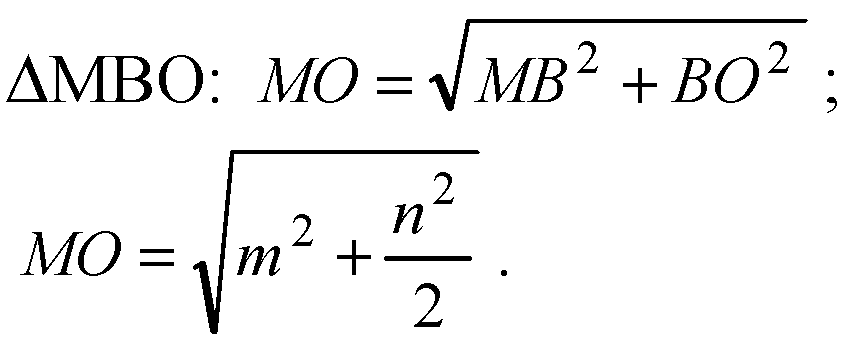
Ответ: а)

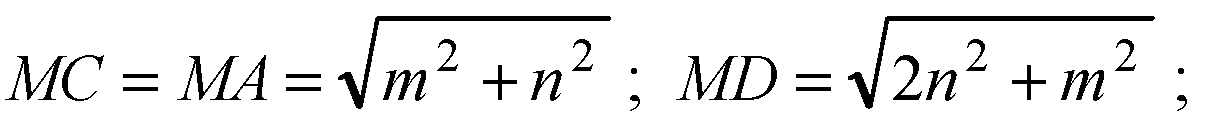
Б)