135. Прямая а перпендикулярна к плоскости α и перпендикулярна к прямой b, не лежащей в этой плоскости. Докажите, что b II α

Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости → номер 135

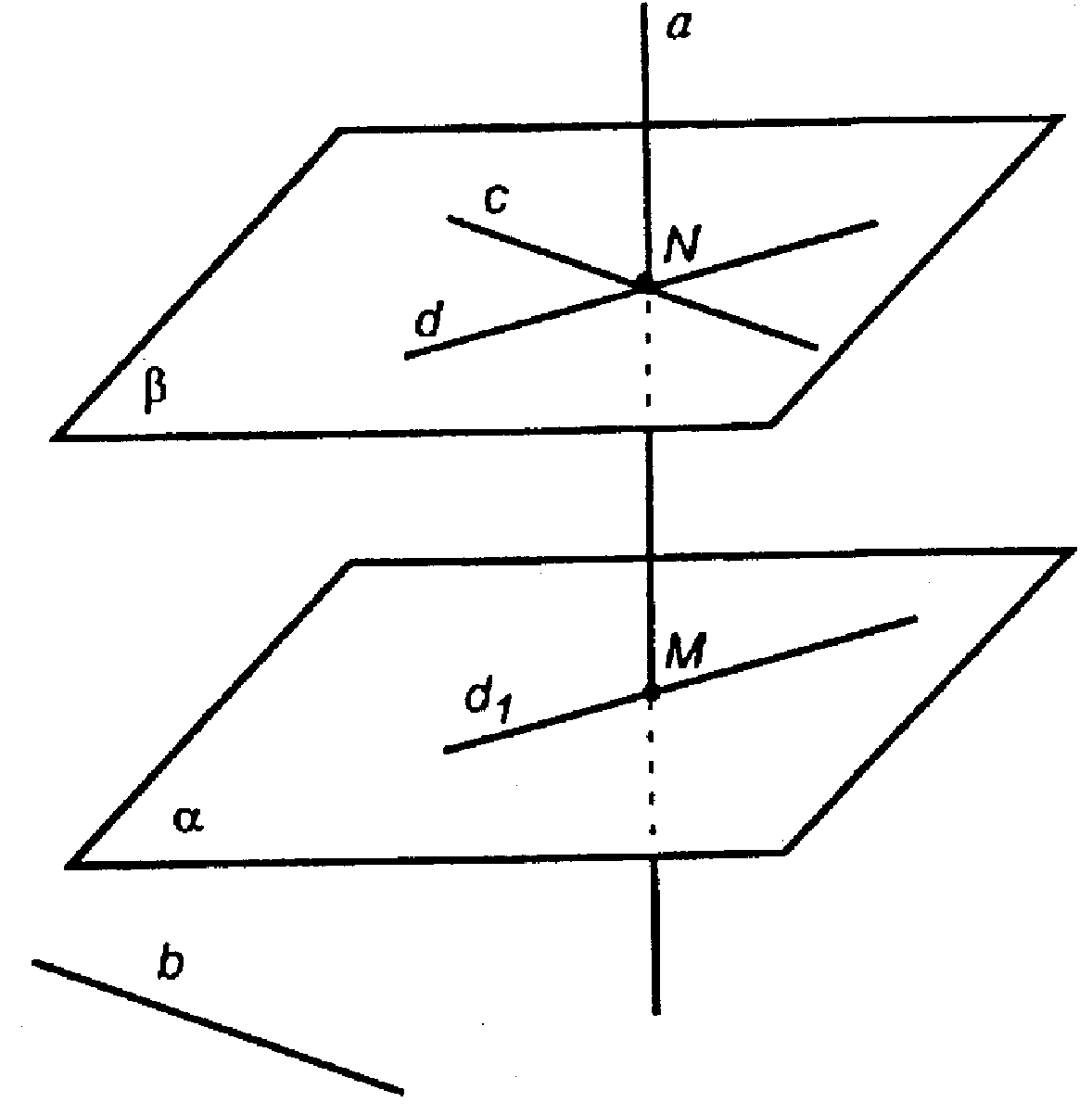
Дано:

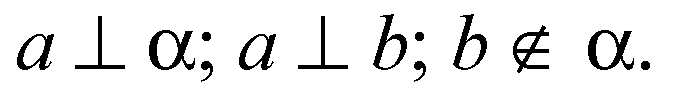
Решение:

Пусть М — точка пересечения а с α. N ∈ a.

Проведем через т. N прямую c || b.

В пл. α через т. М проведем прямую d1.

Через т. N проведем прямую d || d1. а ⊥ d1, d1 || d, поэтому а ⊥ d.

Т. о. а ⊥ β (Через т. А проходит единственная β, перпендикулярная к а).

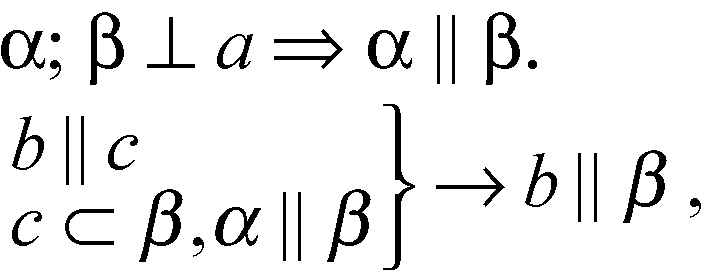
Следовательно,

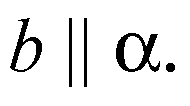
Что и требовалось доказать.