Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости → номер 136
Дано:
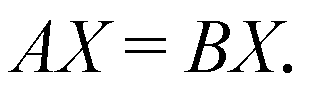
Решение:
Выясним, чем является Г М Т точек равноудаленных от А и В.
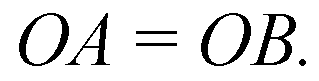
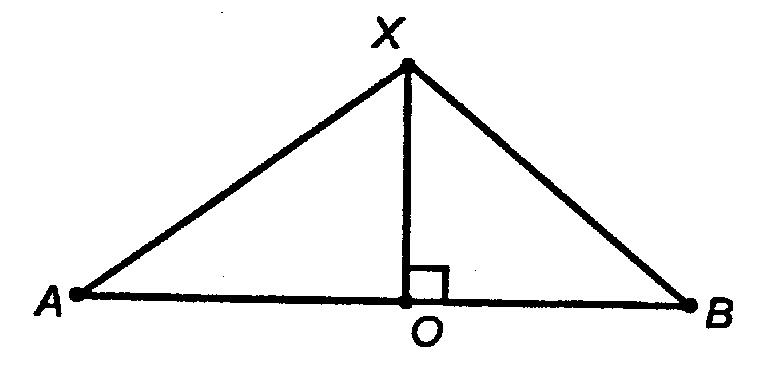
Утверждение задачи следует из того, что в каждой плоскости, проходящей через АВ и некоторую xn (см. рисунок), xn будет серединным перпендикуляром к АВ, то есть ГМТ, равноудаленный от А и В.
