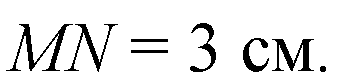Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 141
Решение:
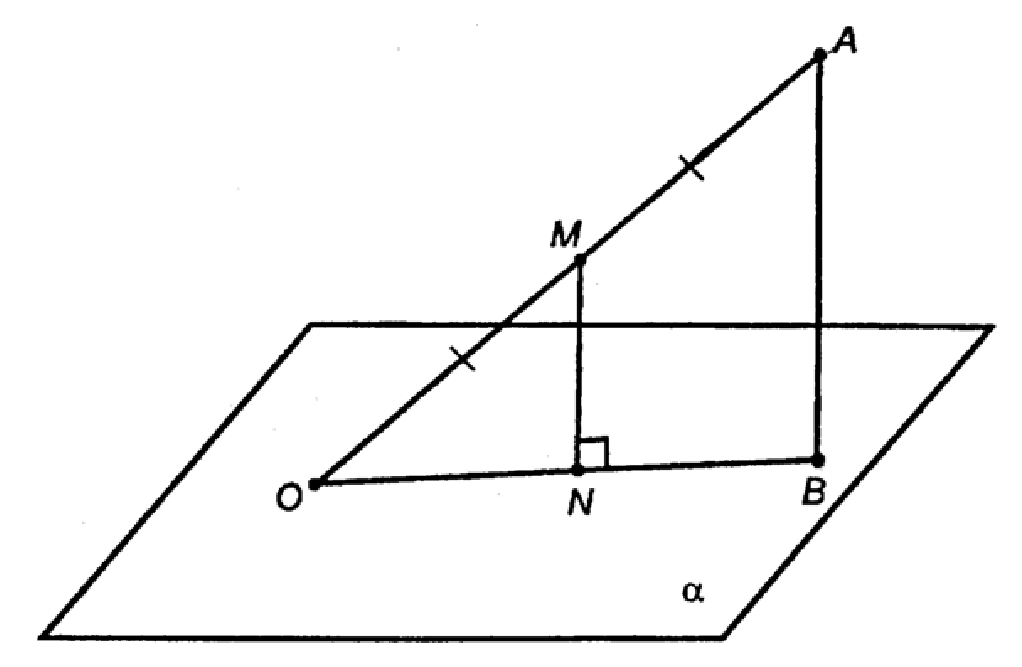
АО — отрезок, О∈а, р(А, α)= 6 см, ОМ=МА. Найти р(М, α).
Проведем АВ ⊥ α и отрезок ВО. Получим плоскость АОВ.
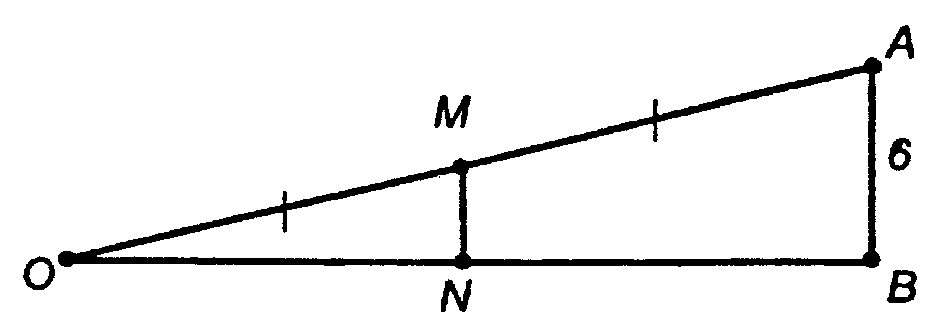
Из т. М проведем в пл. АОВ отрезок MN || AB, т. N — пересечение отрезка с пл. а. Доказано (п. 21), что N ∈ ОВ, т. е. MN с пл. АОВ (см. учебник).
MN — средняя линия ΔОАВ (по теореме Фалеса ON = NB).
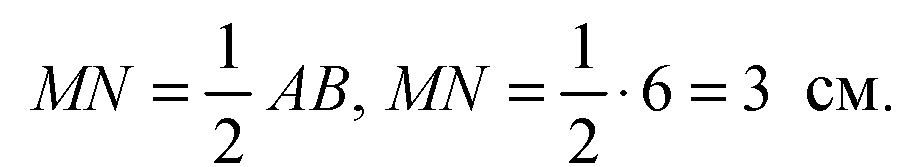
Ответ: