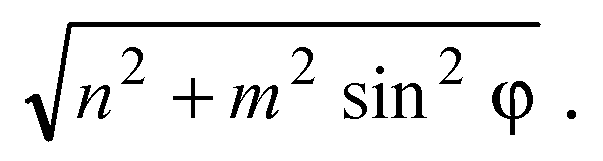Глава II Перпендикулярность прямых и плоскостей. §2 Перпендикуляр и наклонные. Угол между прямой и плоскостью. → номер 156 156. Один из катетов прямоугольного треугольника ABC равен т, а острый угол, прилежащий к этому катету, равен φ. Через вершину прямого угла С проведена прямая CD, перпендикулярная к плоскости этого треугольника, CD = n. Найдите расстояние от точки D до прямой АВ.
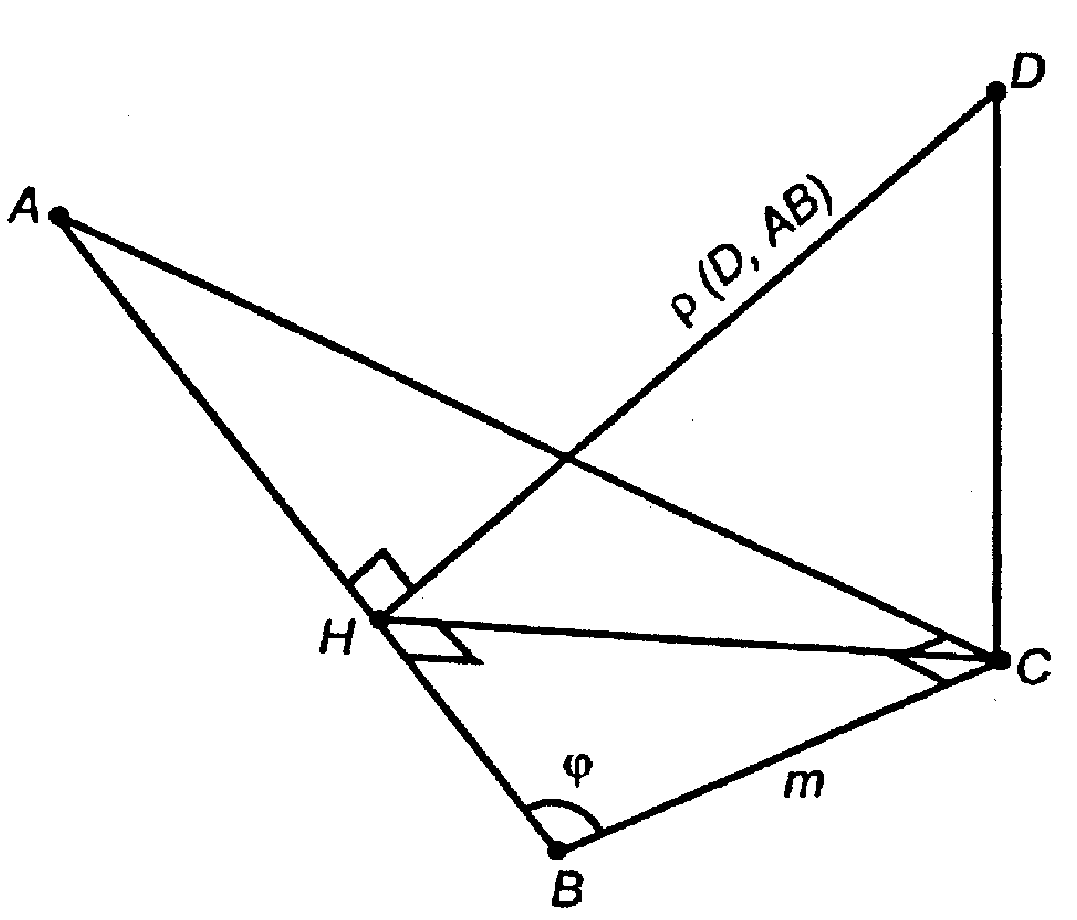
Проведем СН ⊥ АВ и DH.
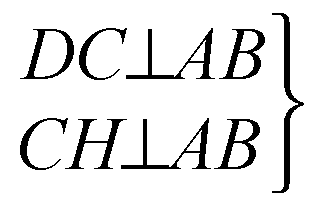
По теореме о 3-х перпендикулярах DH ⊥ AB
(CH — проекция, DC — перпендикуляр).
DH — искомое расстояние.
Из ΔАВС: СН = m • sinφ (соотношение в прямоугольном треугольнике).
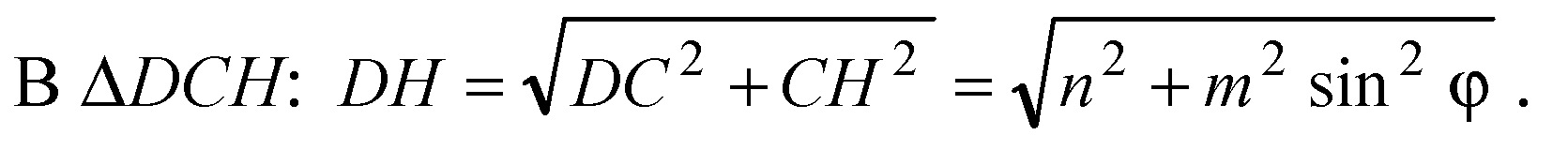
Ответ: