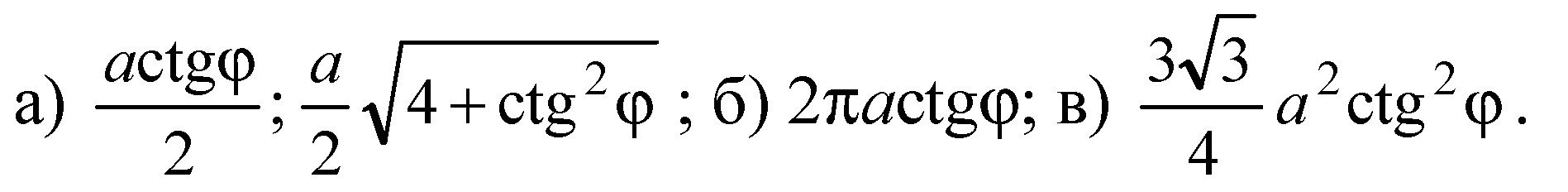Дополнительные задачи к главе II Перпендикулярность прямых и плоскостей. → номер 204 204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр О этого треугольника, ОМ = а, ∠MCO = φ. Найдите: а) расстояние от точки М до каждой из вершин треугольника ABC и до прямых АВ, ВС и СA; б) длину окружности, описанной около треугольника ABC; в) площадь треугольника ABC.
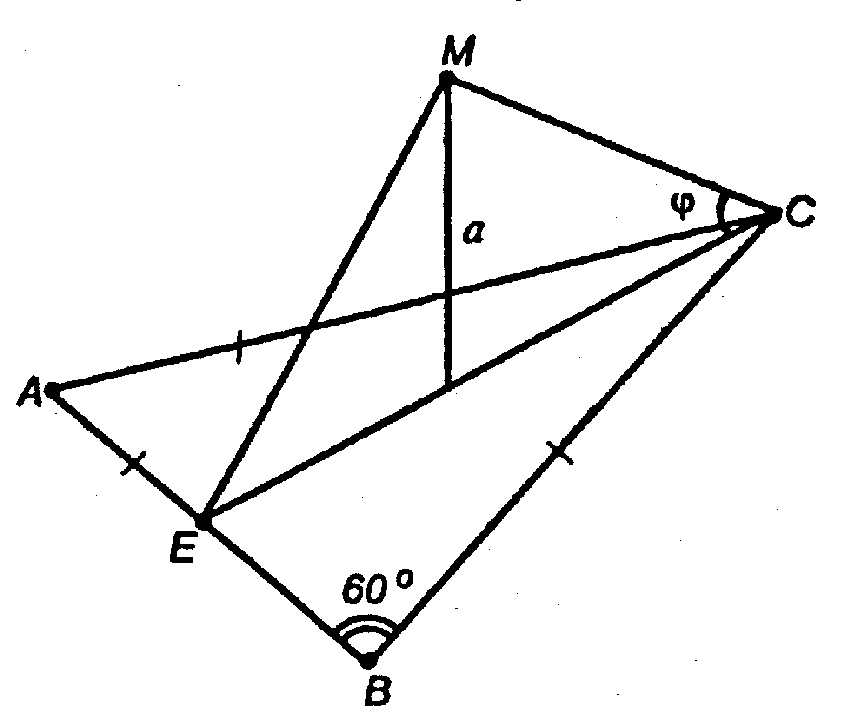
Решение:
А)
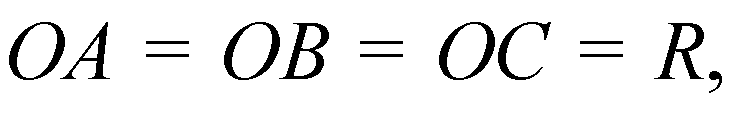
R — радиус описанной окружности около
ΔABC, поэтому
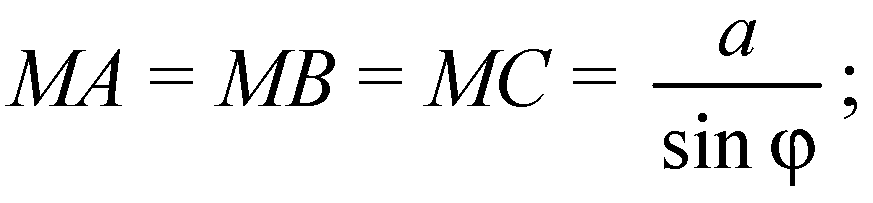
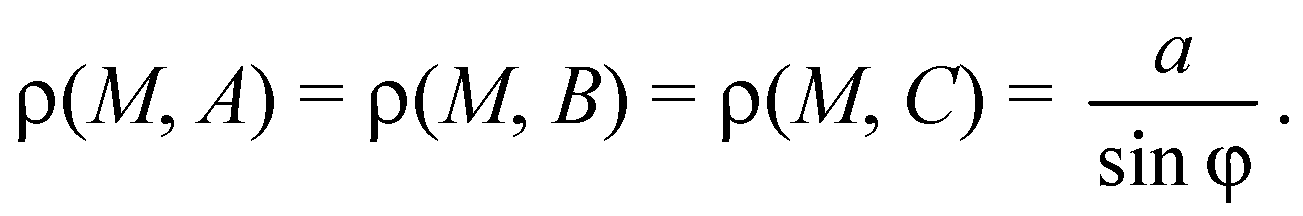
В правильном ΔABC:
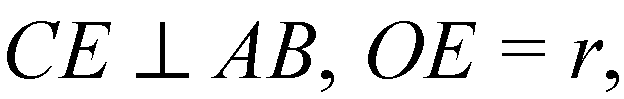
R — радиус вписанной ок
Ружности.
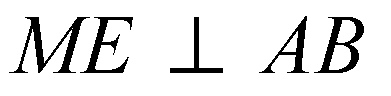
(по теореме о 3-х перпендикулярах), следовательно,
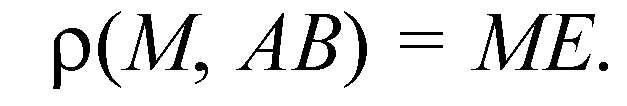
Раз ΔABC — правильный, то
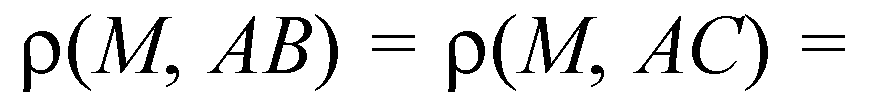
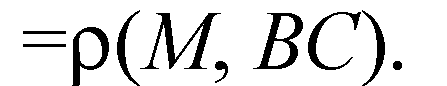
В ΔABC:
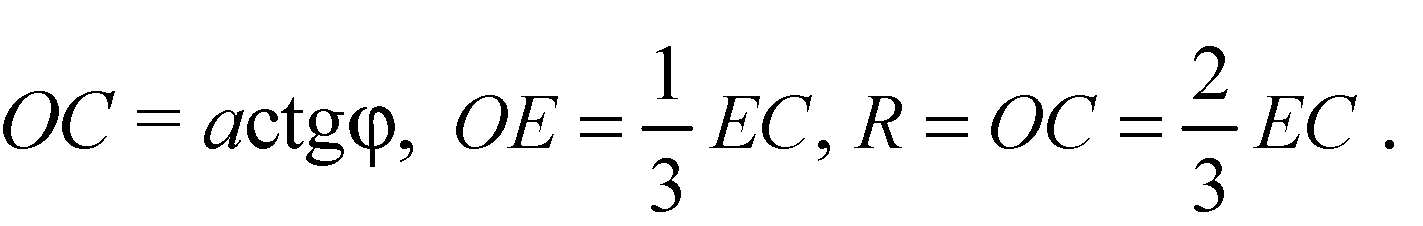
Из уравнения
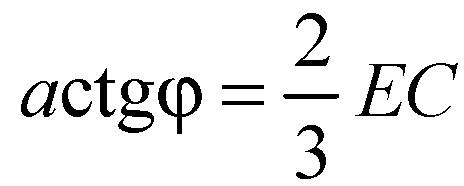
Получаем, что
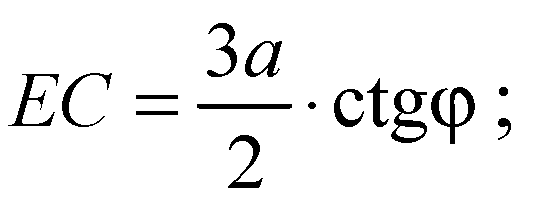
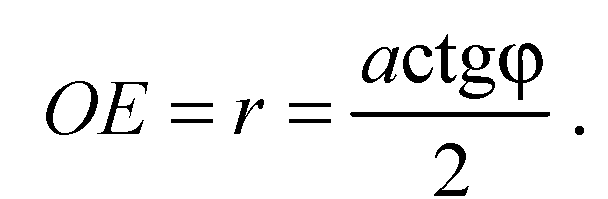
Из ΔMOE:
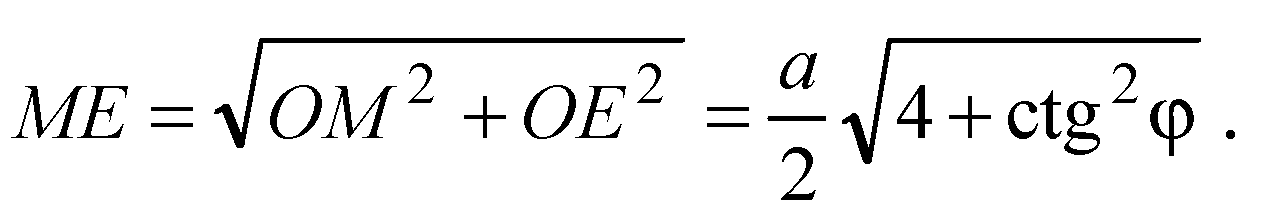
Б) Длина окружности
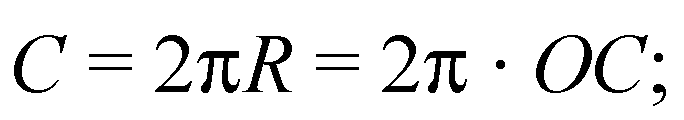
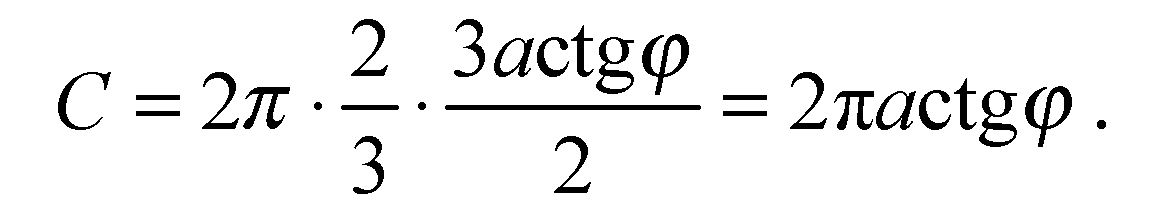
В)
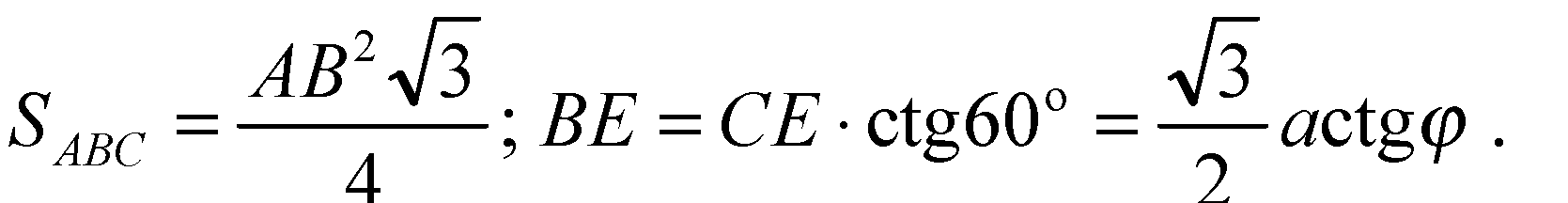
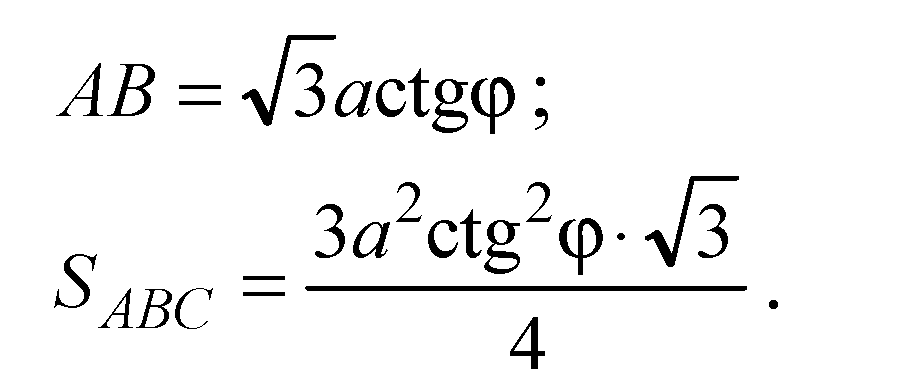
Ответ: