Глава III Многогранники. Дополнительные задачи → номер 295 295. Основанием наклонного параллелепипеда ABCDA1B1C1D1 является ромб. Боковое ребро СС1 составляет равные углы со сторонами основания CD и СВ. Докажите, что: a) CC1⊥BD; б) BB1D1D — прямоугольник; в) BD⊥АА1С1; г) плоскости АА1С1 и BB1D1 взаимно перпендикулярны.
а) Так как ∠С1СВ = = ∠С1СD, то проекция С2 точки С1 на плоскость ABCD попадает на биссектрису ∠BCD (рис. 186). Но биссектриса угла BCD — это AC и значит С2С⊥BD. Тогда по теореме о трех перпендикулярах следует, что СС1⊥BD.
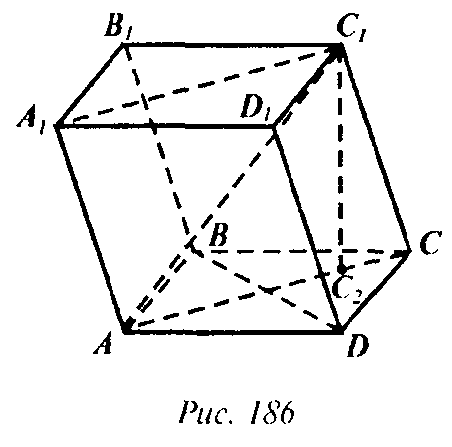
Б) BB1D1D — параллелограмм и ВВ1 ⊥ ВD (так как ВВ1 || СС1 и СС1 ⊥ ВD), значит ВВ1D1D — прямоугольник. в) ВD ⊥ А1С (так как ВD ⊥ АС как диагонали ромба) и ВD ⊥ АА1 (так как ВD || СС1). Тогда по признаку перпендикулярности прямой и плоскости следует, что ВD ⊥ AA1C1. г) Плоскость BB1D проходит через прямую B1D1, перпендикулярную к плоскости АА1С1 так как B1D || BD и BD⊥AA1C1. Поэтому по теореме п. 23 следует, что AA1C1⊥BB1D1.
