Глава III Многогранники. Дополнительные задачи → номер 297 297. Основанием треугольной призмы АВСА1В1С1 является правильный треугольник ABC, BD — высота этого треугольника, а вершина А1 проектируется в его центр. Докажите, что: a) A1BD⊥АА1С1; б) АА1O⊥ВВ1С; в) грань ВВ1С1С — прямоугольник.
a)A1C1⊥BD, так как A1C1||AC и AC⊥BD, и A1O⊥A1C1, так как A1O⊥AC и AC||A1C1. Поэтому по признаку перпендикулярности прямой и плоскости А1С1 ⊥ DA1B. Значит по теореме п. 23 следует, что АА1С1 ⊥ A1BD.
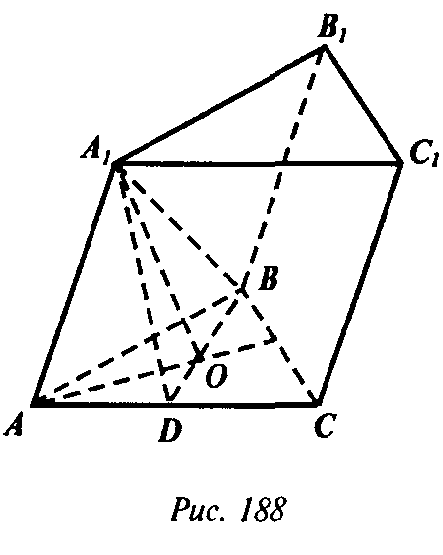
Б) Аналогично п. а) ВС ⊥ АА1О. Поэтому по теореме п. 23 АА1О ⊥ВВ1С. в) АО — проекция АА1 на плоскость ABC и АО ⊥ ВС. Следовательно по теореме о трех перпендикулярах AA1 ⊥ ВС и, так как AA1|| ВВ1, то ВВ1 ⊥ ВС. Значит параллелофамм ВВ1С1С является прямоугольником.
