304. В правильной четырехугольной пирамиде плоский угол при вершине равен 60°. Докажите, что двугранный угол между боковой гранью и основанием пирамиды вдвое меньше двугранного угла при боковом ребре

Глава III Многогранники. Дополнительные задачи → номер 304

Рассмотрим пирамиду PABCD. О — точка пересечения диагоналей квадрата ABCD (рис. 191). М — середина PC. N — середина CD.

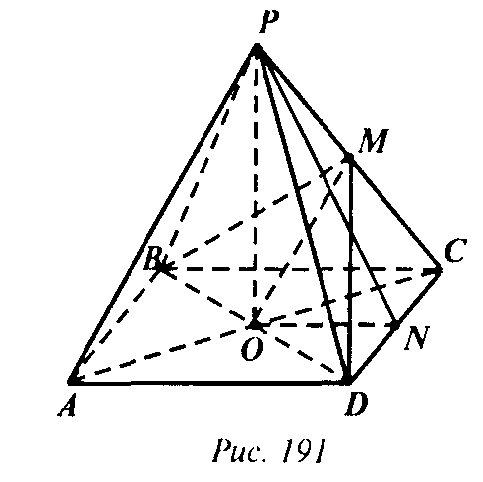
Так как ∠CPD = 60° то равнобедренный треугольник CPD является равносторонним. Поэтому все ребра пирамиды равны между собой. BM=MD, поэтому медиана МО является биссектрисой ΔBMD.

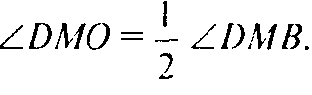
Докажем, что ΔDMO = ΔPNO. Действительно, PN = MD — как медианы равностороннего ΔDPC.

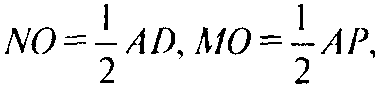
Как средние линии треугольников CAD и СРА. Поэтому NO = МО. Тогда

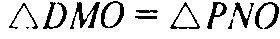
По катету и гипотенузе. Значит

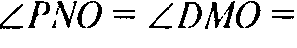
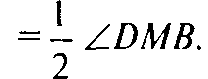
Но ∠PNO — угол между боковой гранью и основанием. a ∠DMB — линейный угол двугранного угла при боковом ребре. Таким образом, требуемое утверждение доказано.