Глава III Многогранники. Дополнительные задачи → номер 307 307. В правильной пирамиде MABCD AM = b, AD = a. а) Постройте сечение пирамиды плоскостью α, проходящей через диагональ BD основания параллельно ребру MA, и найдите площадь сечения. б) Докажите, что точки М и С равноудалены от плоскости α.
а) Пусть точка K — середина MC, Тогда ОК||AM, поэтому точка K лежит в плоскости α. BKD — искомое сечение. ВК = DK (т. к. ΔMBC=ΔMDC). Поэтому OK⊥BD.
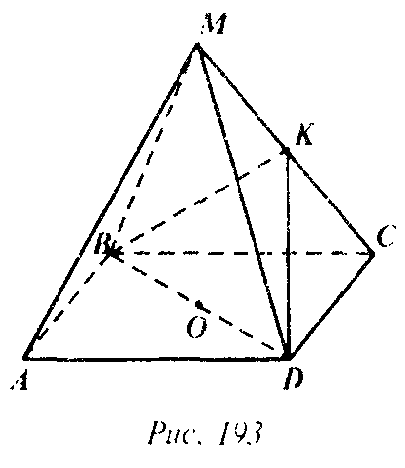
Из ΔСАМ: КО — средняя линия, значит
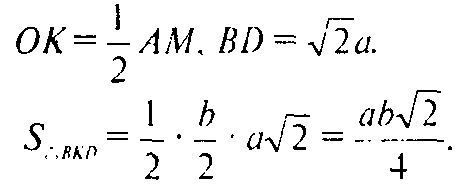
Б) Рассмотрим MM1 — перпендикуляр к плоскости BKD и проведем плоскость M1MC. По теореме п. 23 видно CMM1⊥BDK, поэтому СС1 — перпендикуляр к BDK также лежит в плоскости MM1C. Таким образом C1, K, M1 — лежат на одной прямой. Но тогда ∠MKM1 = ∠CKC1 (как вертикальные) и ΔMKM = ΔCKC1 (по гипотенузе и острому углу). Значит MM1 = CC1, что и требовалось доказать.
