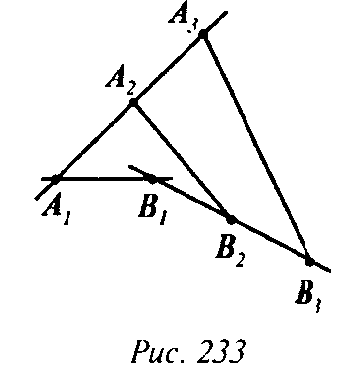
Глава IV. Векторы в пространстве Дополнительные задачи → номер 389 389. На двух скрещивающихся прямых отмечены по три точки: A1, A2, A3 и B1, B2, B3, причем A1A2=k⋅A1A3, В1В2= k⋅В1В3. Докажите, что прямые А1В1, А2В2, A3B3 параллельны некоторой плоскости.
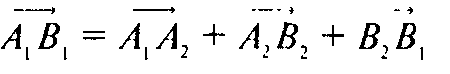
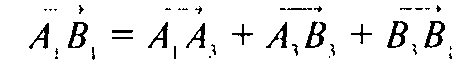
(рис. 233)
Вычтем из первого равенства второе с коэффициентом к. Тогда
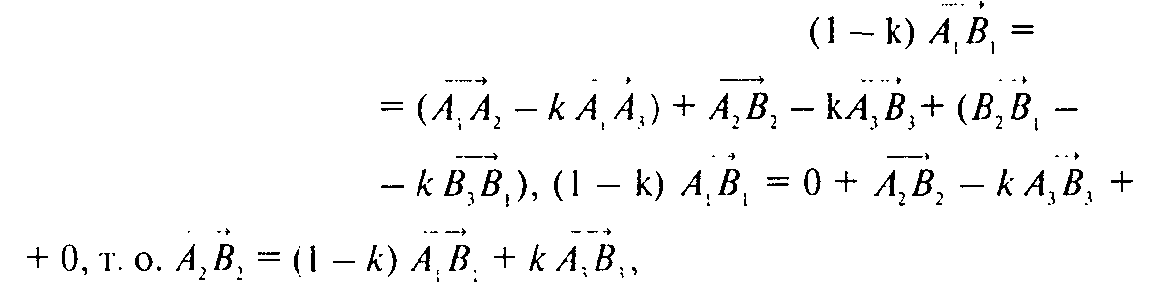
Т. е. векторы
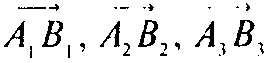
Компланарны, а это и означает, что прямые
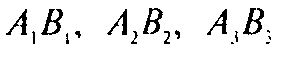
Параллельны одной плоскости.
