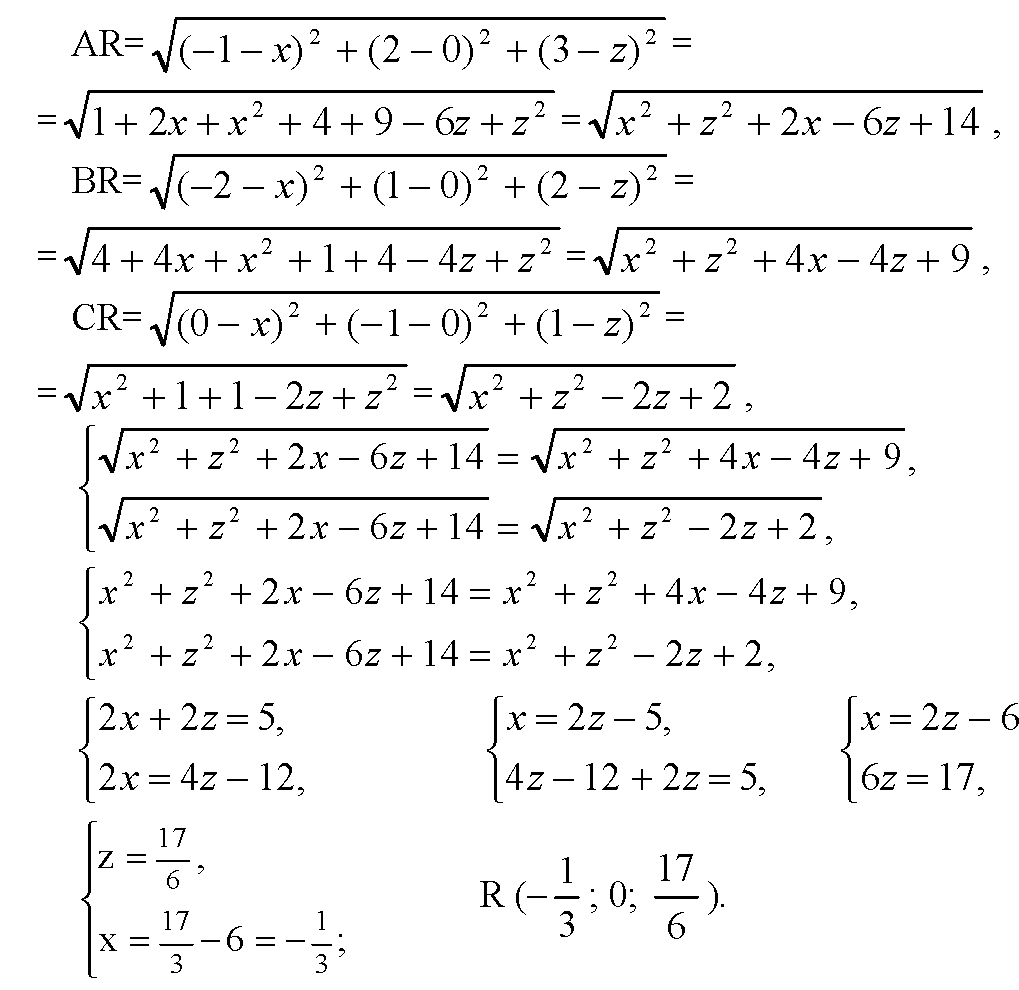438. Даны точки А (— 1; 2; 3), В ( — 2; 1; 2) и С (0; — 1; 1). Найдите точку, равноудаленную от этих точек и расположенную на координатной плоскости: а) Оху; б) Oyz; в) Ozx

Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 438

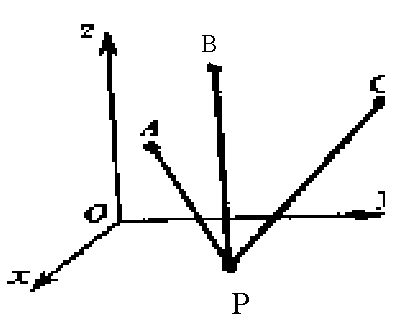
а) Пусть на плоскости Оху точка Р (х; у; 0) равноудалена от А, В и С. Используя формулу

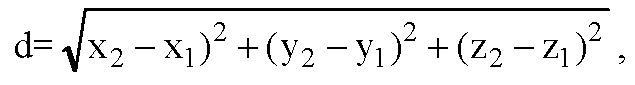
Составим систему уравнений:

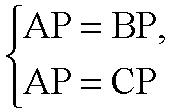
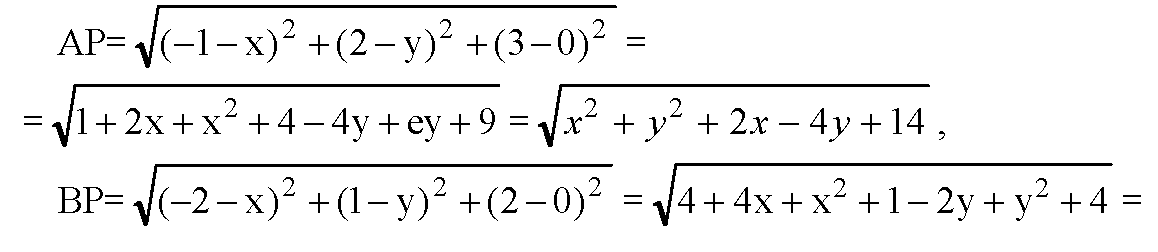
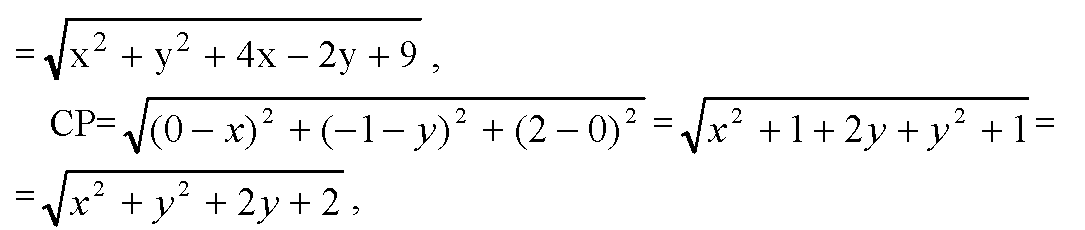
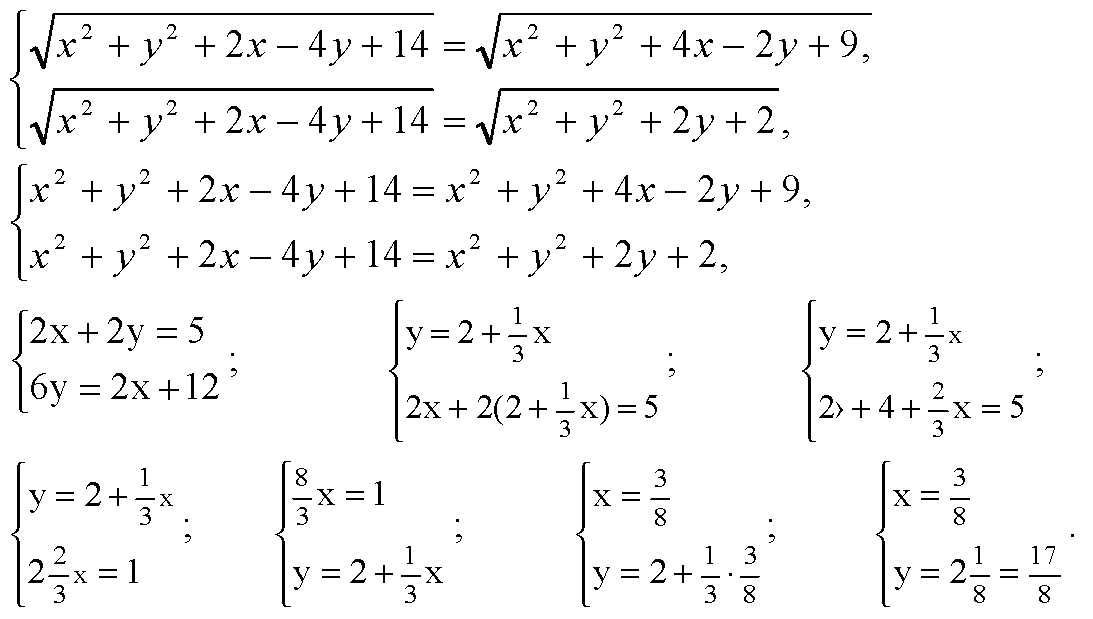
Точка

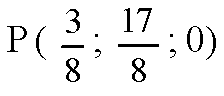
Лежит на плоскости Оху и равноудалена от точек А, В и C.

Б) Пусть на координатной плоскости Oyz точка Q (0; y; z) равноудалена от А, В и С, следовательно

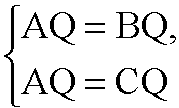
(очевидно, что и BQ=CQ).

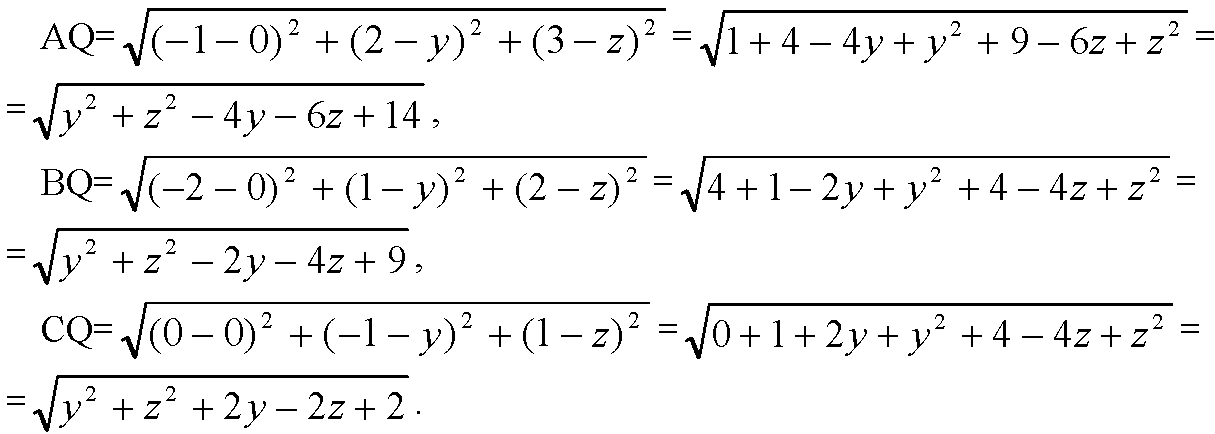
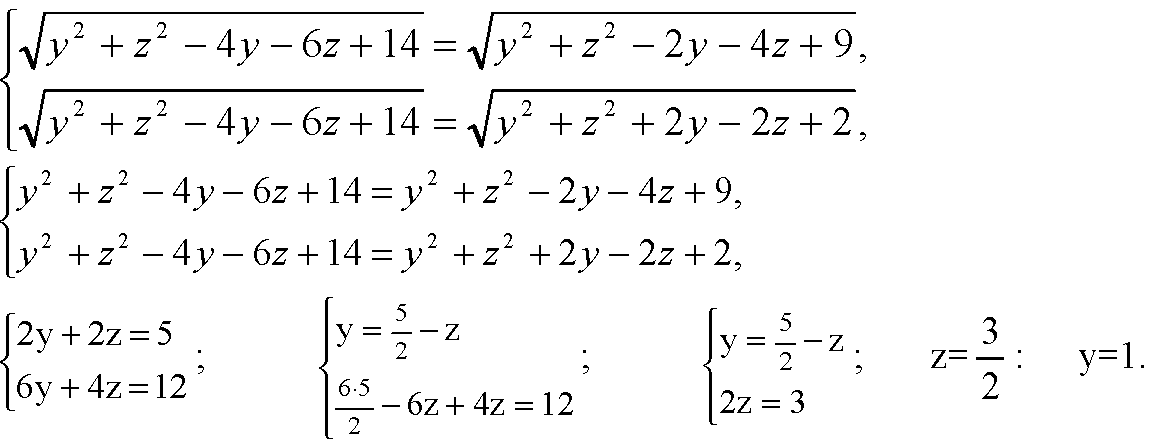
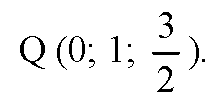
В) Пусть на координатной плоскости Ozx точка R (x, 0; z) равноудалена от точек A, В и С, следовательно