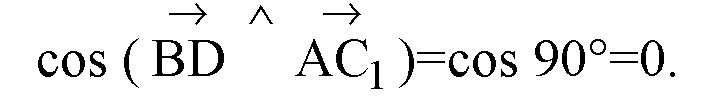Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов → номер 455
Пусть сторона куба равна а, следовательно:
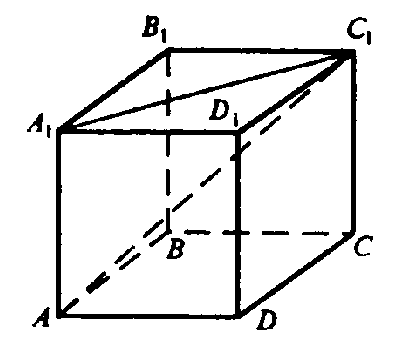
А) В прямоугольном треугольнике АА1С1 положим, АА1= =0, тогда
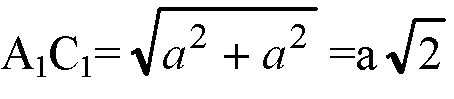
По теореме Пифагора.
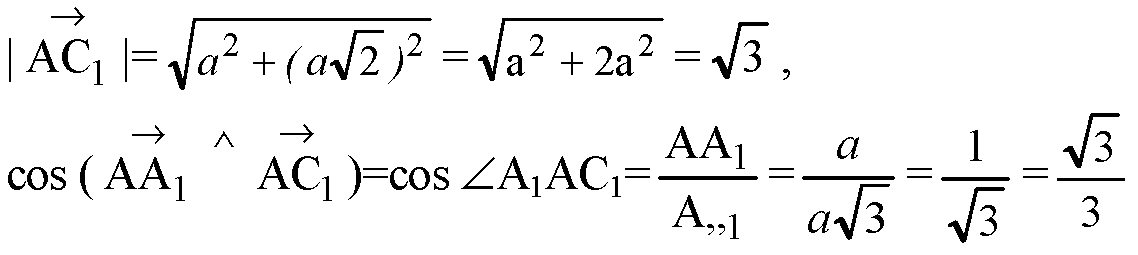
Б) Векторы
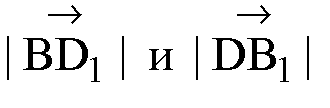
Лежат в плоскости BB1D, сечение куба этой плоскостью — это прямоугольник BB1D1D со сторонами а и а

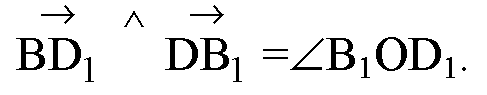
По теореме косинусов в ΔB1OD1:
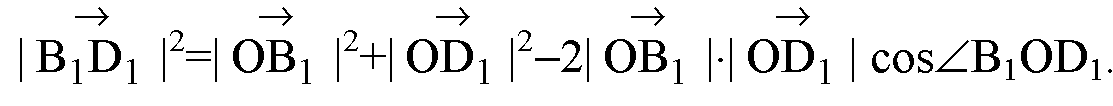
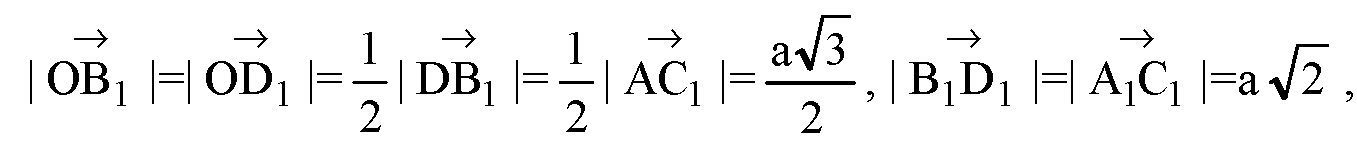
Следовательно
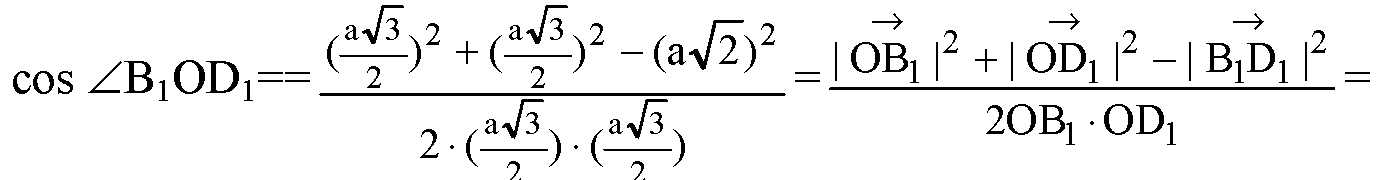
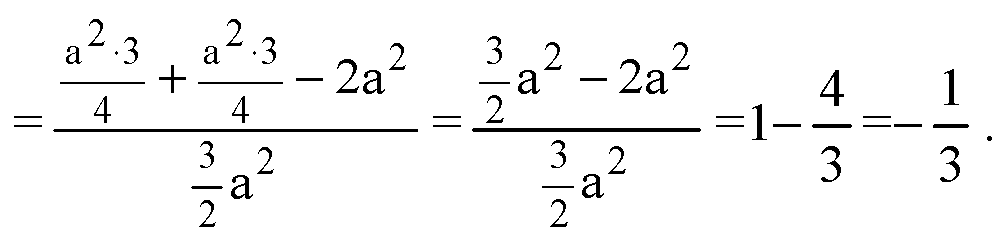
В)
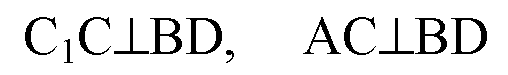
(no свойству
Диагонали квадрата).
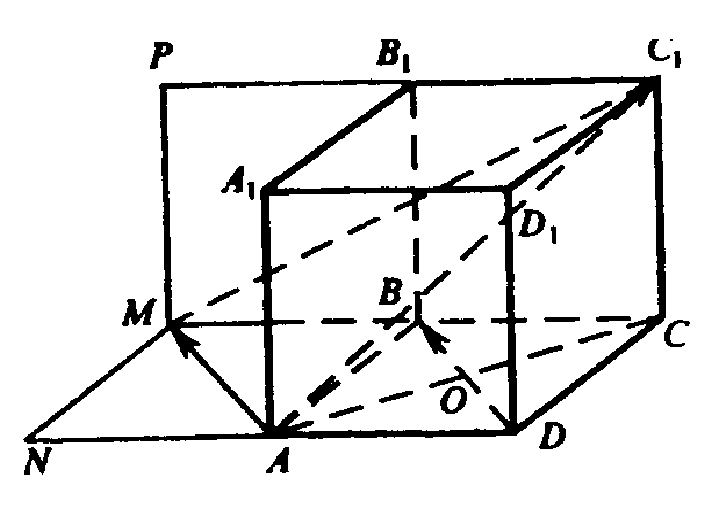
Следовательно, BD перпендикулярно плоскости АС1С, тогда, BD ⊥ AC1,