Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов → номер 463
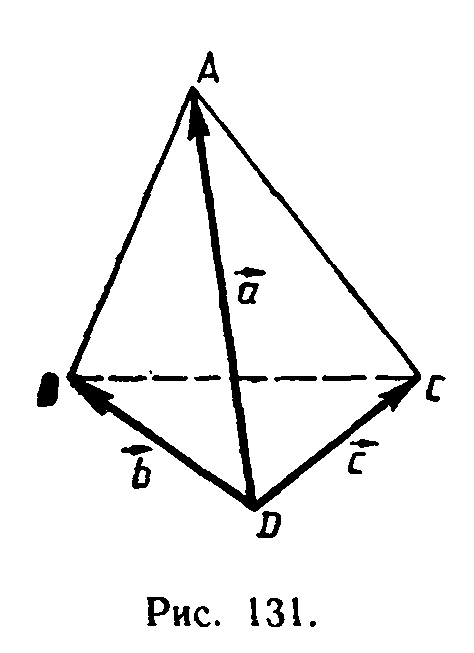
Решение. Введем векторы a = DA, b = DB, c = DC (рис. 131). Тогда АВ = b — а, АС = с — а, ВС = с —b. По условию AD⊥ВС и BD⊥AC, поэтому a⊥(c — b) и b⊥(c-a). Следовательно, а(с — b) = 0 и b(с — а) — 0. Отсюда получаем ac = ab и bc = ba. Из этих двух равенств следует, что ас = bc, или (b—а)с = 0. Но b — a = AB, c = DC, поэтому АВ DC = 0, и, значит, AB⊥CD, что и требовалось доказать.
