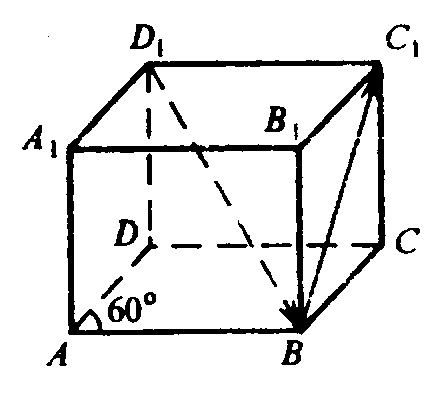
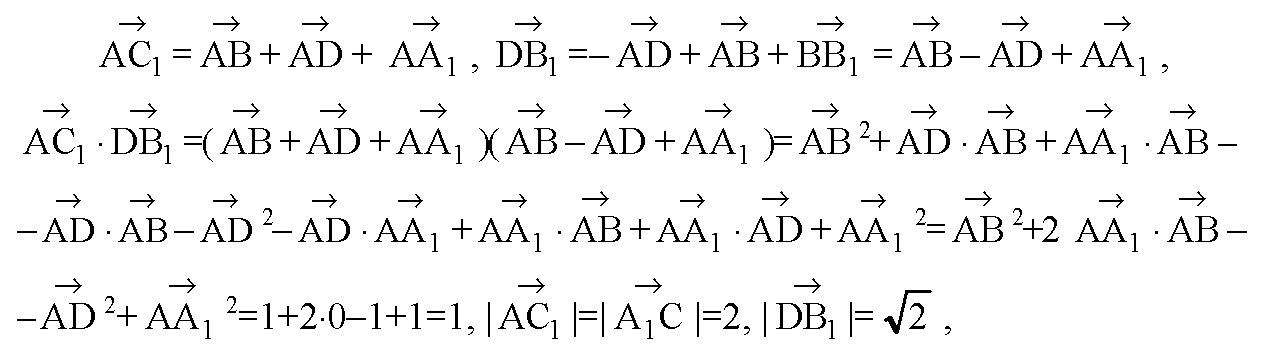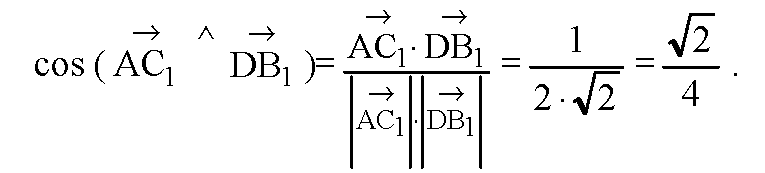Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов → номер 462 462. В параллелепипеде ABCDA1B1C1D1 AA1=AB = AD=1, ∠DAB = 60°, ∠A1AD=∠A1AB = 90°. Вычислите: a) BA⋅D1C1; б) BC1⋅D1B; в) AC1⋅AC1; г) |DB1|; д) |A1C|; e) cos (DA1^D1B); ж) cos (AC1^DB1).
Воспользуемся свойством параллелепипеда.
X)

По свойству параллелепипеда, то
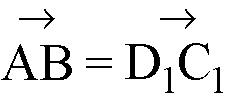
,).
2)
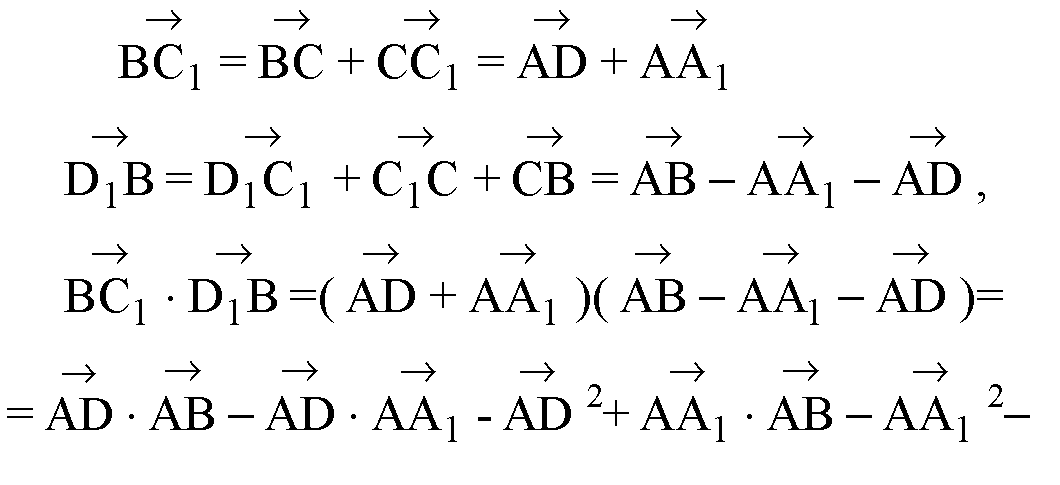
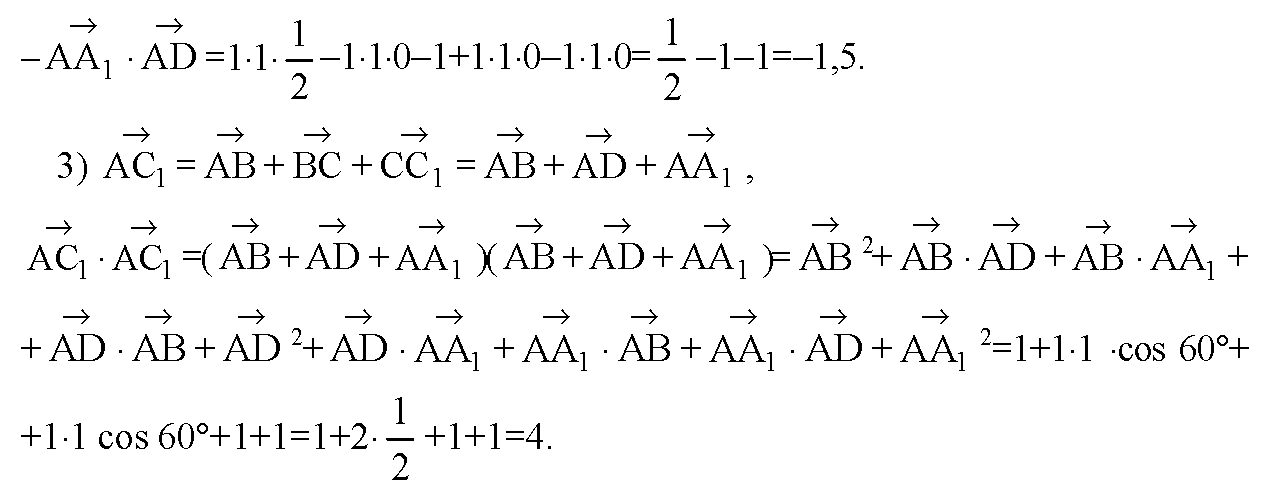
4) В основании параллелепипеда лежит ромб ABCD, у которого
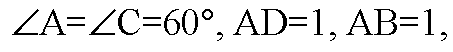
Откуда следует, что
А)
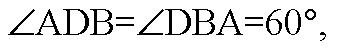
Б) DB=1.
В ΔDBB1:
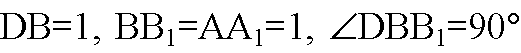
(BB1 ⊥ плоскости основания, т. к. АА1 ⊥ плоскости основания и ВВ1 || AA1)
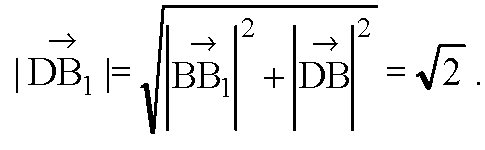
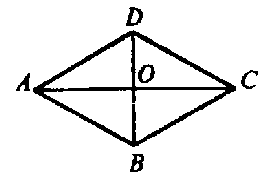

5) Рассмотрим основание параллелепипеда. АС=2АО, где О — точка пересечения диагоналей ромба. АО — высота в равностороннем ΔADB,
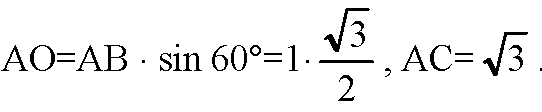
В прямоугольном ΔАА1С
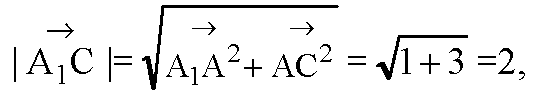
6)
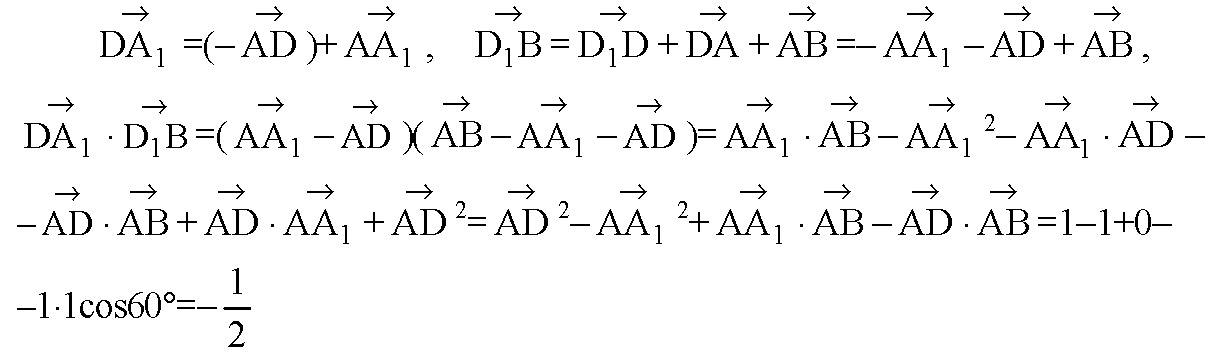
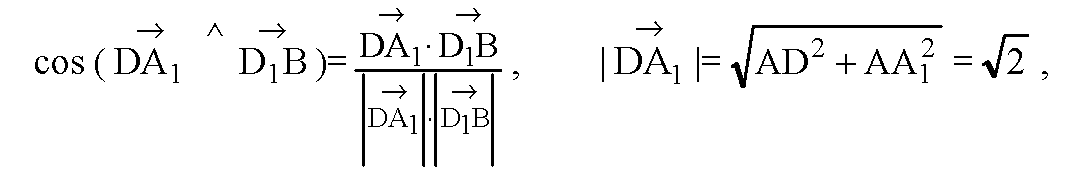
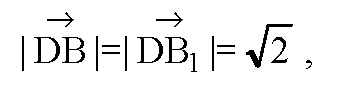
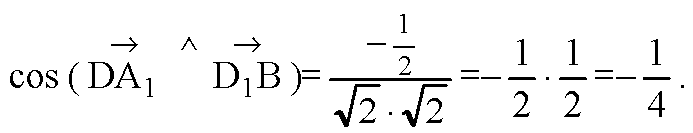
7)