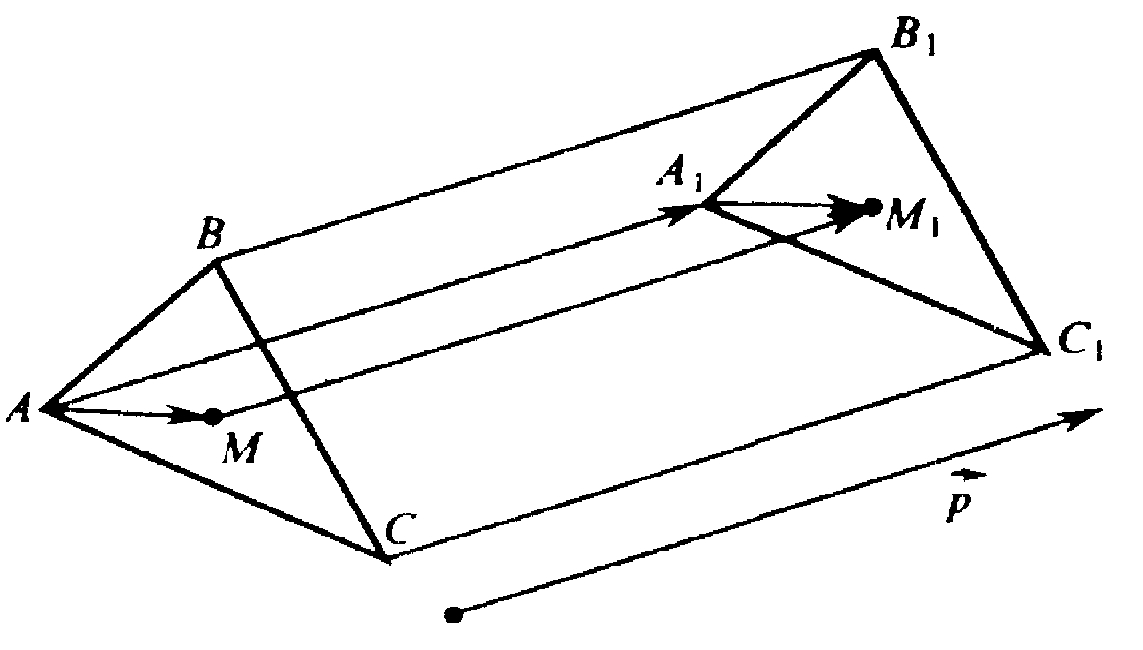
Глава V. Метод координат в пространстве. § 3. Движения → номер 485 485. Треугольник A1B1C1 получен параллельным переносом треугольника ABC на вектор р. Точки M1 и М — соответственно точки пересечения медиан треугольников A1B1C1 и ABC. Докажите, что при параллельном переносе на вектор р точка М переходит в точку М1.
Параллельный перенос — это движение, тогда АВ=А1В1, ВС=В1С1, АС=А1С1. Отсюда ΔABC=ΔА1В1С1. Проведем отрезки AM и А1М1. AM=А1М1.
Для плоского четырехугольника АММ1А1 имеем:
АМ||А1М1, АМ=А1М1, следовательно,
АММ1А1 — параллелограмм, AA1 = MM1 = р.