Глава V. Метод координат в пространстве. § 3. Движения → номер 486
а) а — данная прямая.
Возьмем на прямой а точки А, В, С. При движении они перейдут в точки А1, В1, Q соответственно, причем АВ=А1В1, ВС=ВА и АС=А1C1. Необходимо доказать, что А1, В1, С1 лежат на одной прямой.
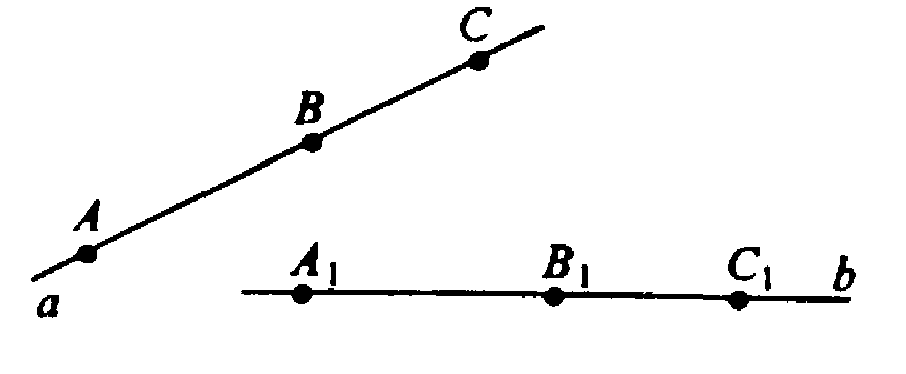
A1C1=A1B1+B1C1. Такое равенство верно, если все три точки — лежат на одной прямой; иначе по неравенству треугольника А1C1 < А1В1+В1С1. В силу произвольного выбора точек А, В и С доказательство справедливо для любых других точек, таким образом, движение переводит прямую в прямую.
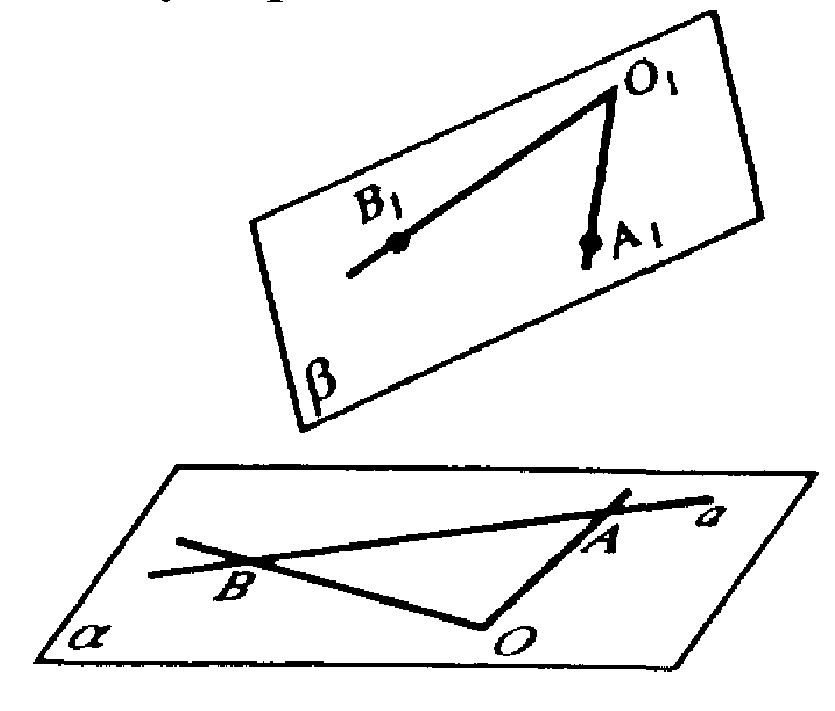
Б) В плоскости α проведем прямую а и возьмем точку О ∉ а. Проведем из точки О отрезки, пересекающие прямую а в точках А и В.
При движении: О → О1, А → А1, так что ОА=О1А1; В → В1, так что ОВ=О1В1 По аксиоме: через две пересекающиеся прямые проходит плоскость и притом только одна.
