Дополнительные задачи к главе V Метод координат в пространстве → номер 493
Для решения задачи установим, можно ли вектор a разложить по векторам b и c, т. е. существуют ли m и n, удовлетворяющие условию
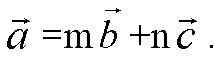
А)
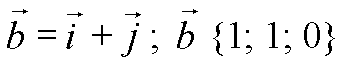
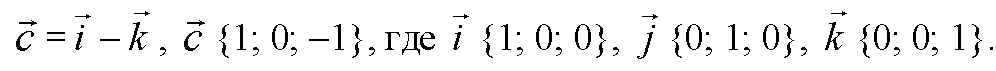
Запишем равенство
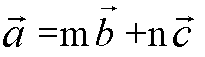
В координатах:
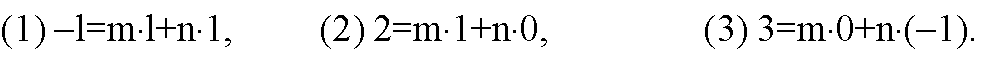
Равенства (x), (2) и (3) выполняются при m=2, n=-3, т. е., векторы а, b и c компланарны.
Б)
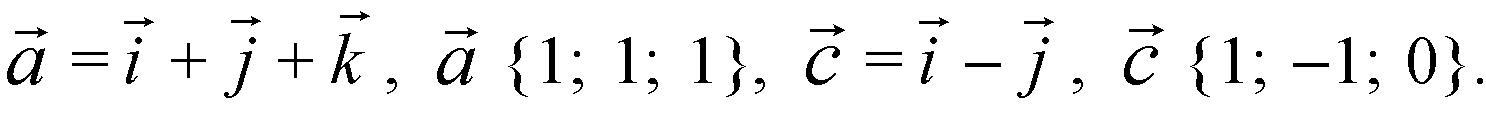
Запишем равенство
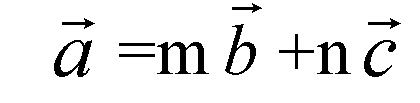
В координатах:
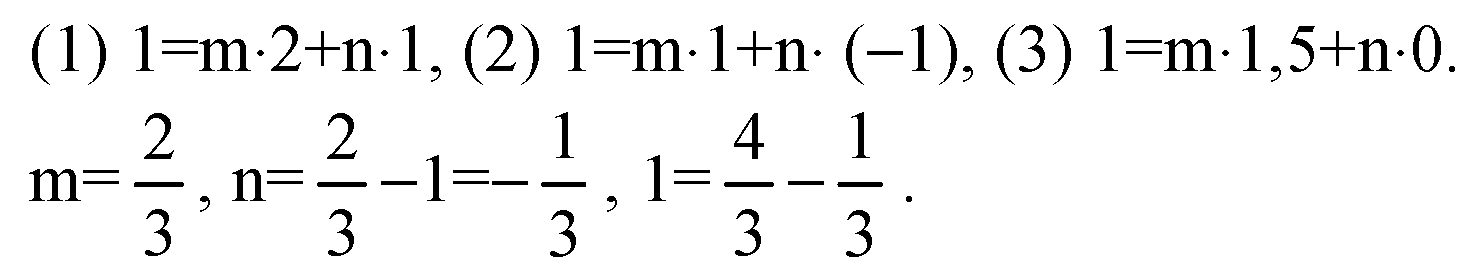
Равенства (1), (2) и (3) выполняются при
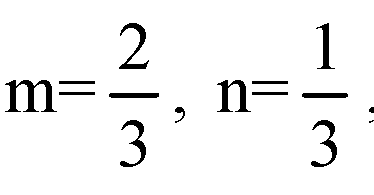
Т. е., векторы a,
B и c компланарны. в) Запишем равенство
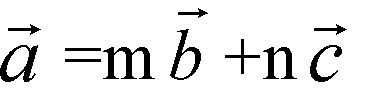
В координатах.
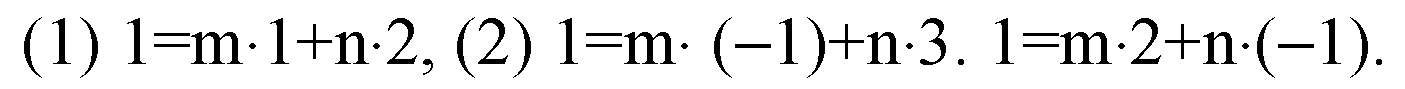
Система уравнений не имеет решений. Т. е. векторы a,
B и c не компланарны.
