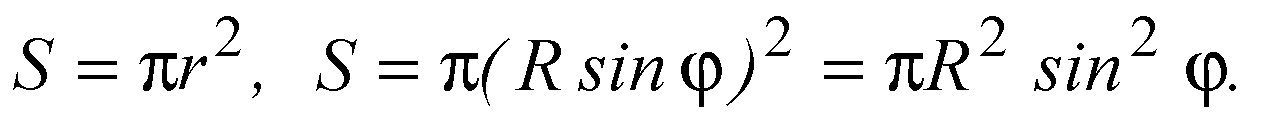Глава VI. Цилиндр, конус и шар § 3. Сфера → номер 590
С — точка, касания плоскости α со сферой; плоскость с — касательная к сфере; β образует с α угол φ; β пересекается с шаром по окружности, диаметр которой СВ.
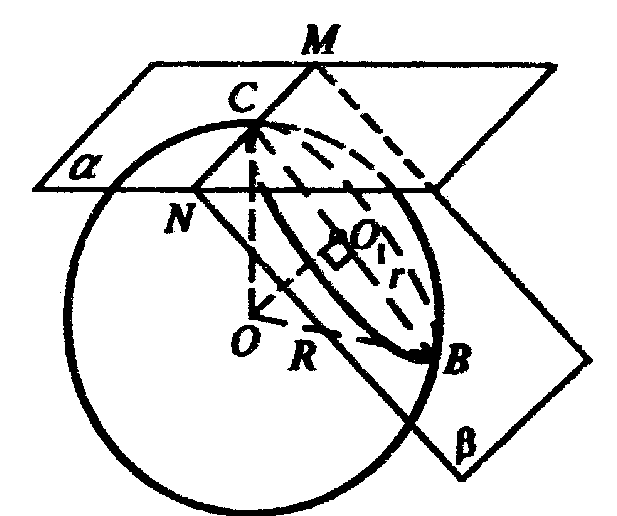
Построим ОО1 ⊥ СВ, соединим точку О с точками С и В. ΔОО1С = ΔОО1B (прямоугольные, ОО1 — общий катет, ОС = ОВ = R). Тогда, СО1 = О1B, точка О1 — центр окружности,
По которой плоскость β пересекает шар.
Построим сечение шара плоскостью СОВ. φ — угол между плоскостями α и β.
∠OCB = 90o -φ, поскольку ΔBOC — равнобедренный, то ∠OBO1 = 90o -φ.
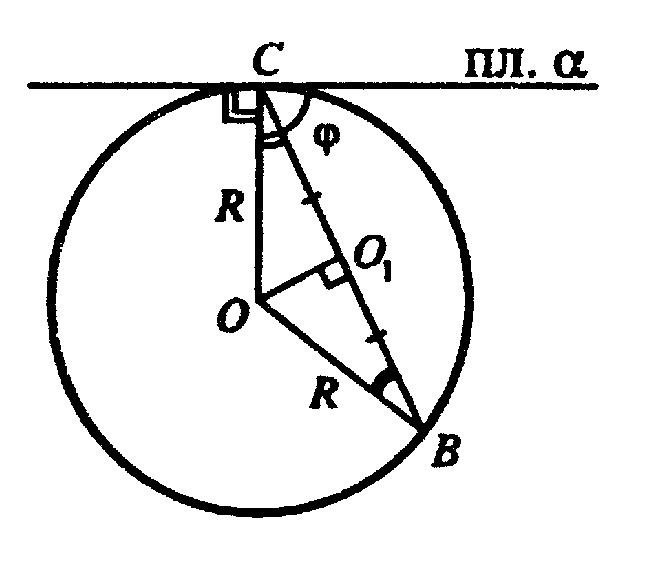
Из ΔОО1B:
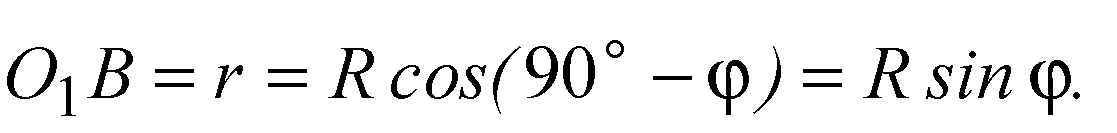
Площадь сечения шара