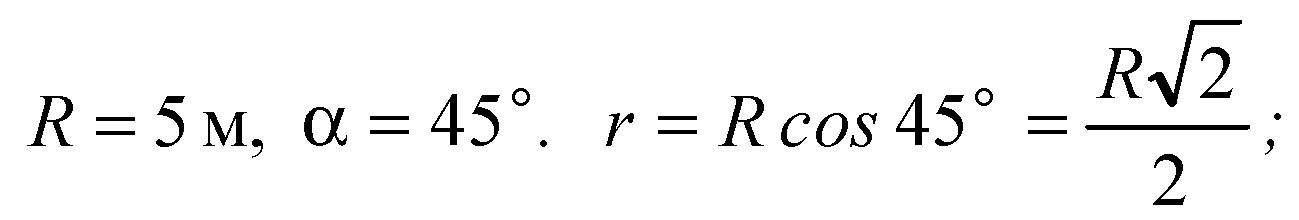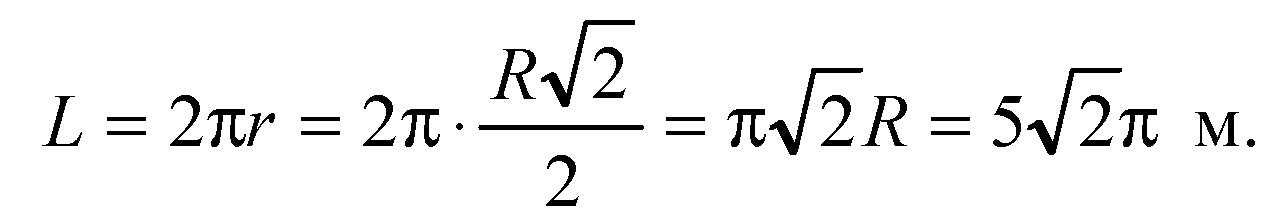Глава VI. Цилиндр, конус и шар § 3. Сфера → номер 589
Опустим перпендикуляр ОО1 к плоскости сечения, соединим точку О1 с точками В и С (точка С получается в результате продолжения отрезка ВО1 до пересечения со сферой).
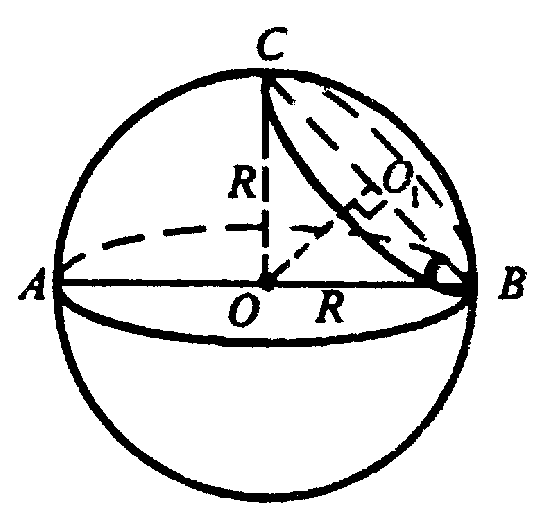
ΔСОВ — равнобедренный, в нем ОО1 ⊥ СВ, тогда,
ОО1 тоже является медианой, СО1=О1В.
Точка О1 равноудалена от точек С и В, лежащих на окружности, по которой сечение пересекает сферу. Точка О1 — центр окружности, ∠OBO1 = α. Пусть O1B = r, тогда
А)
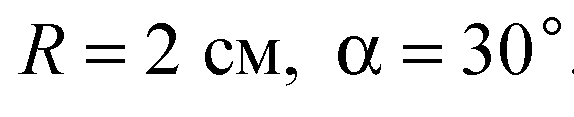
Из ΔОО1 B:
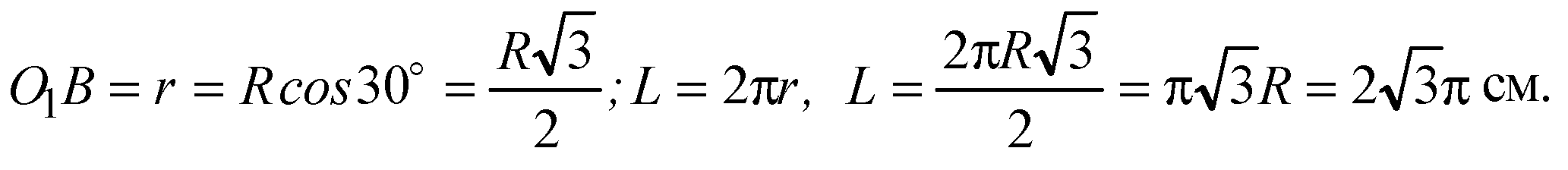
Б)