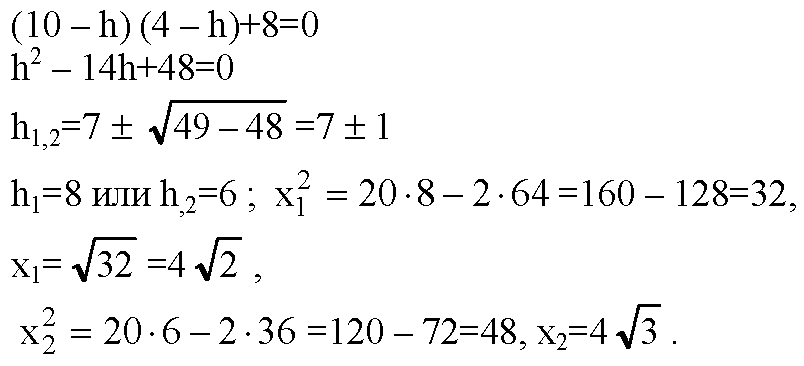Разные задачи на многогранник, цилиндр, конус и шар → номер 641
Продолжим высоту пирамиды РН до пересечения со сферой в точке Q. PQ — диаметр и центр описанной сферы лежит на высоте НР, или на ее продолжении за точку Н. Соединим отрезком точку А с точкой Н. Рассмотрим сечение плоскостью APQ.
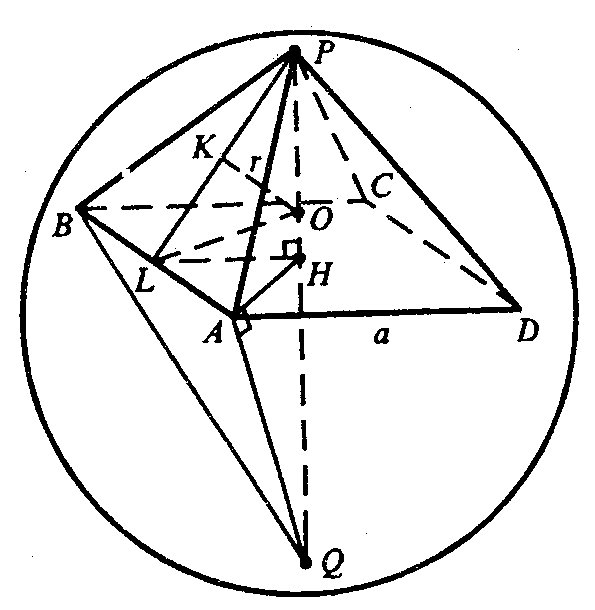
∠QAP=90° так как опирается на диаметр, Из подобия ΔHPA и ΔHAQ,
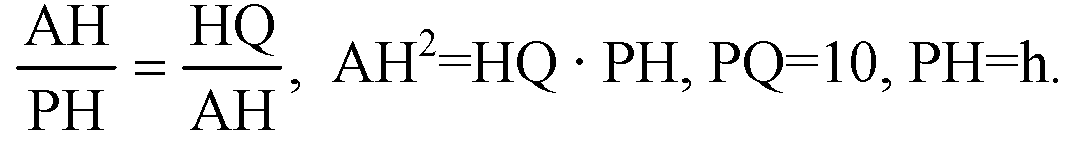
Примем х — сторона основания, следовательно,
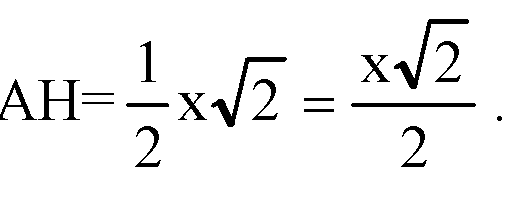
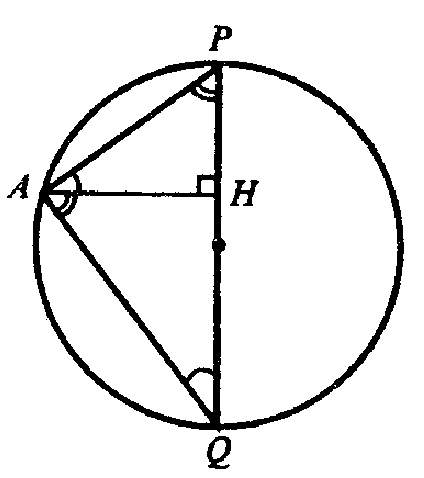
Следовательно,
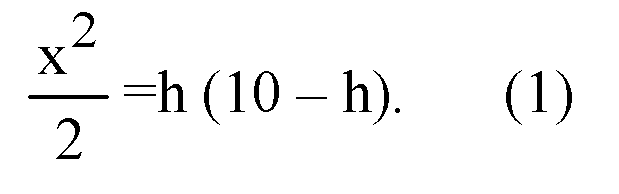
Построим HL ⊥ AB, отрезок PL.
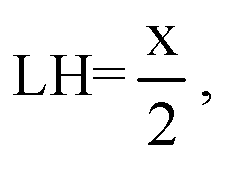
Плоскость PLH ⊥ плоскости
АВР. Пусть О — центр вписанной сферы, ОК ⊥ PL.
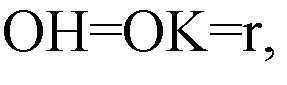
OL — биссектриса ∠HLP.
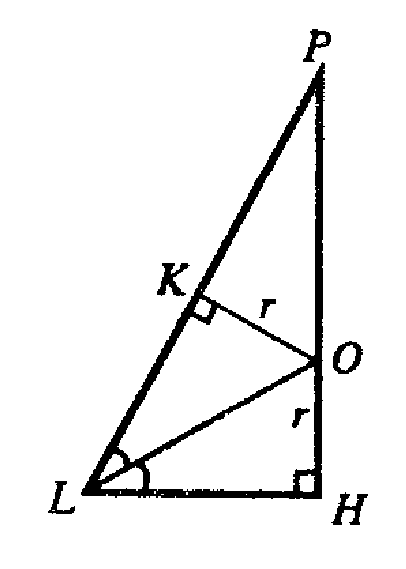
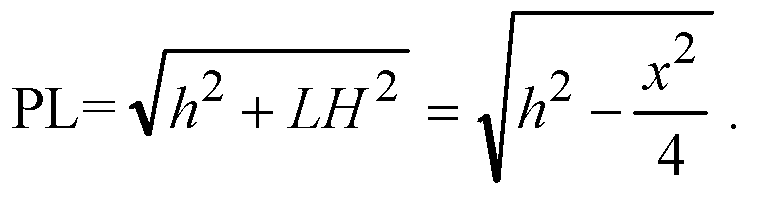
Обозначим ∠HLP= φ.
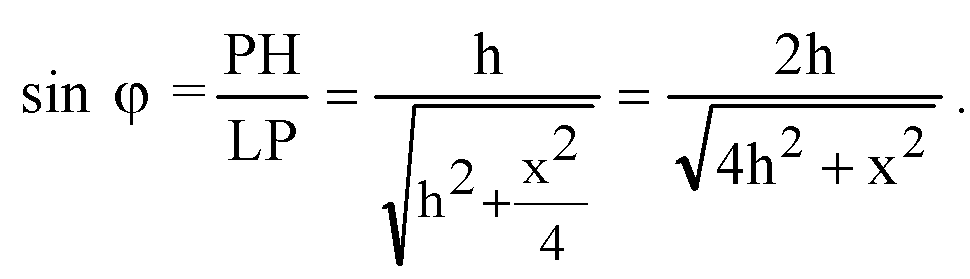
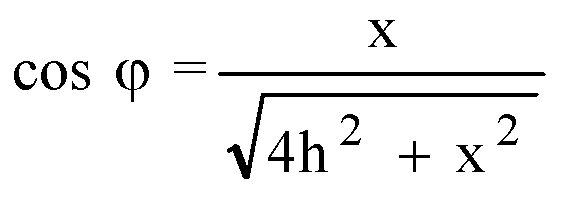
Из ΔOLH:
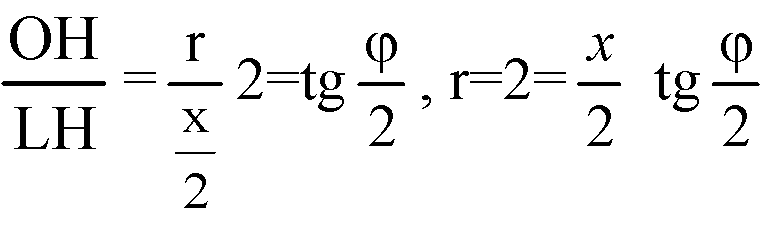
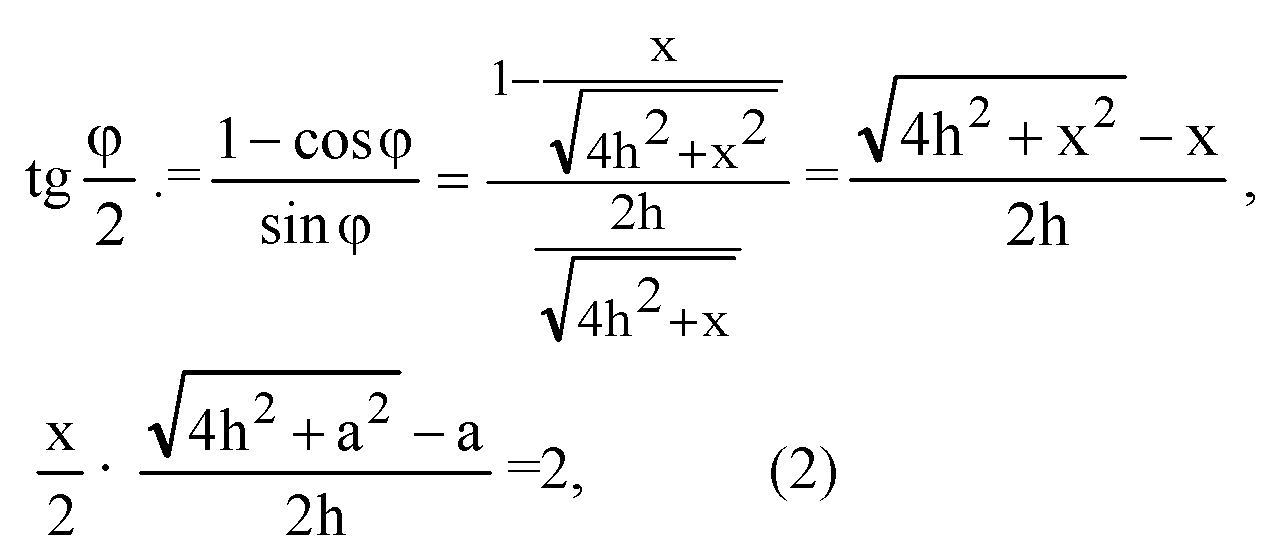
Решим систему:
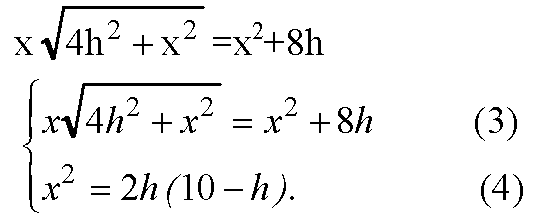
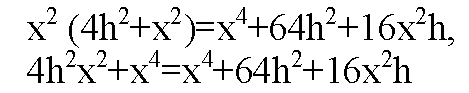
Разделим все на 4h, h ≠ 0
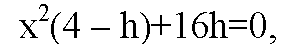
Подставим х2 из (4)
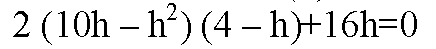
Разделим обе части на 2h, h ≠ 0