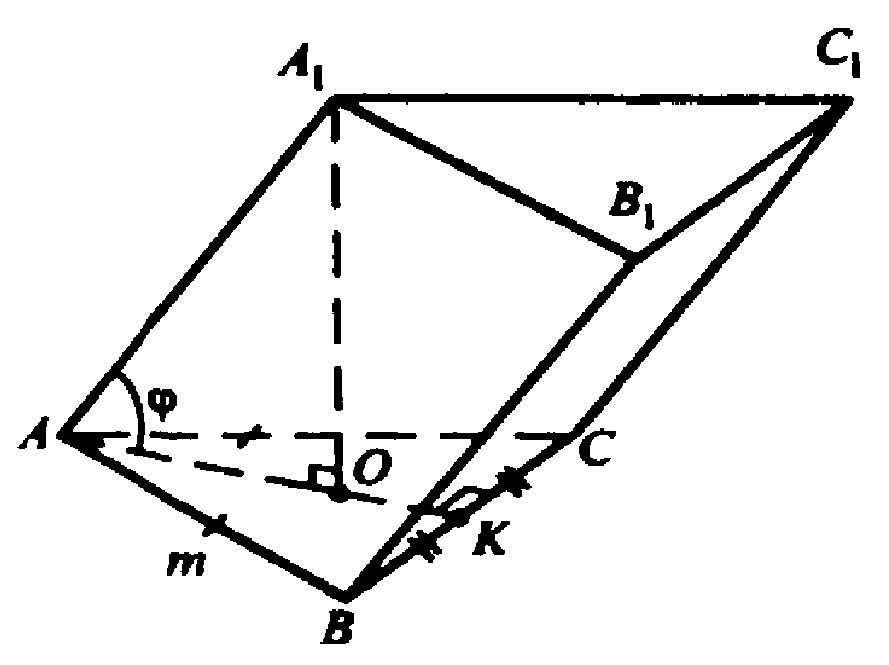
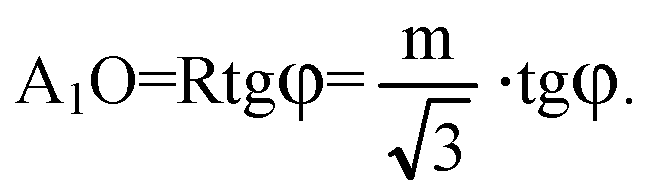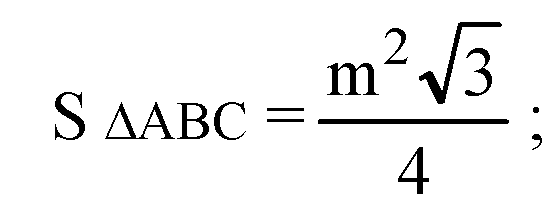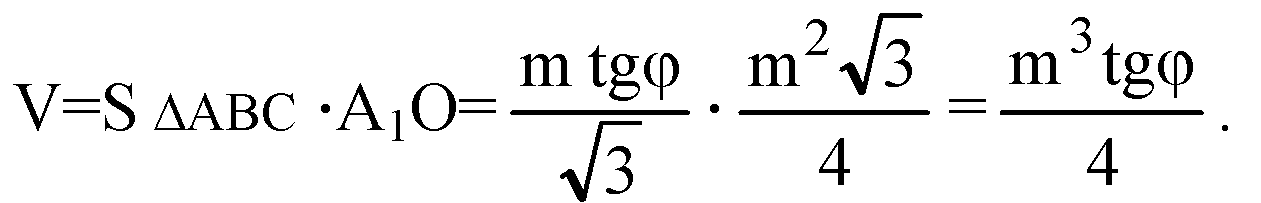Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса → номер 678 678. Основанием призмы АВСА1В1С1 является равносторонний треугольник ABC со стороной m. Вершина А1 проектируется в центр этого основания, а ребро АА1 составляет с плоскостью основания угол φ. Найдите объем призмы.
Построим А1О ⊥ плоскости АВС, точка О — центр правильного ΔАВС. Отрезок ОА — радиус описанной около ΔАВС окружности.
По теореме синусов:
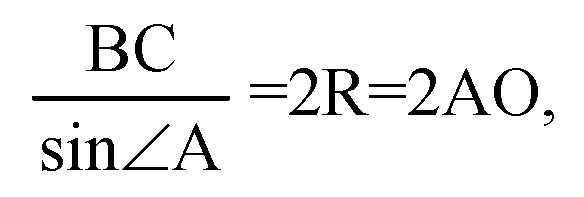
Отсюда
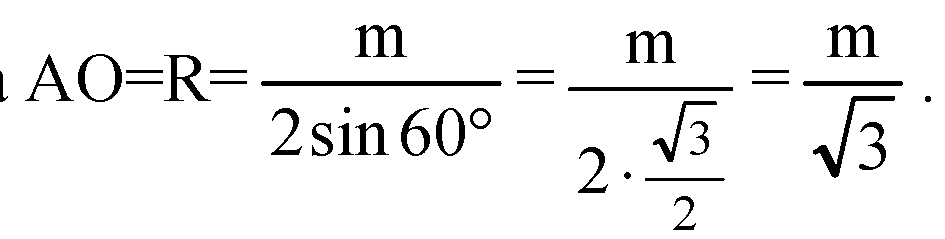
Из прямоугольного ΔА1ОА найдем высоту призмы