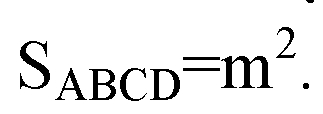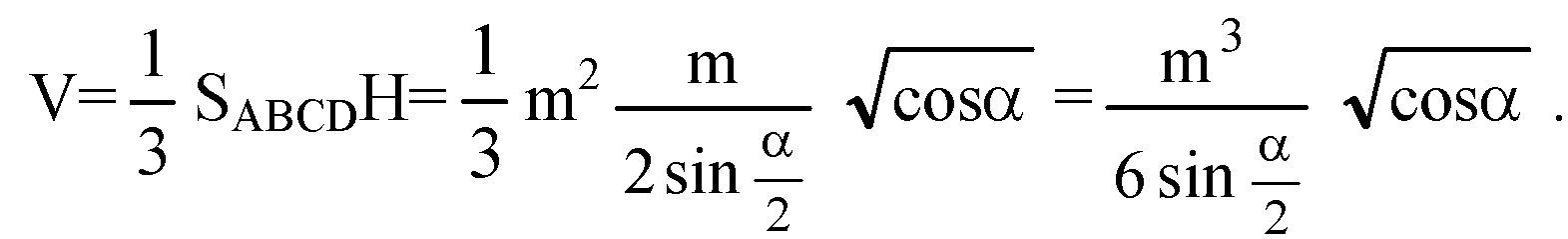Глава VII. Объемы тел. § 3. Объём наклонной призмы, пирамиды и конуса → номер 688
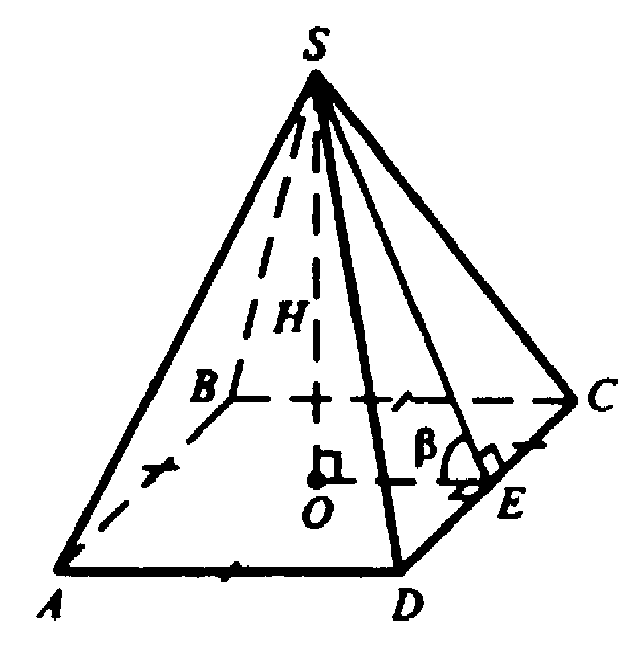
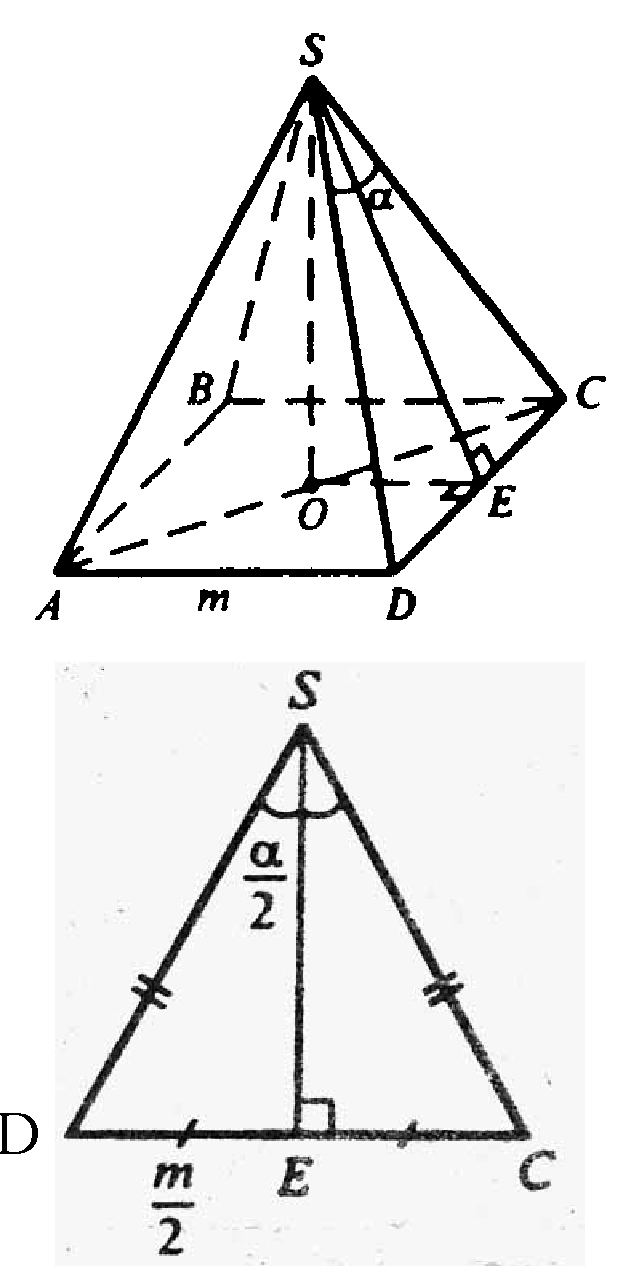
Пусть О — точка пересечения диагоналей. Построим ОЕ⊥DC. По теореме о трех перпендикулярах
SE⊥DC. Таким образом, ∠OES=β — линейный угол двугранного угла при основании.
А)
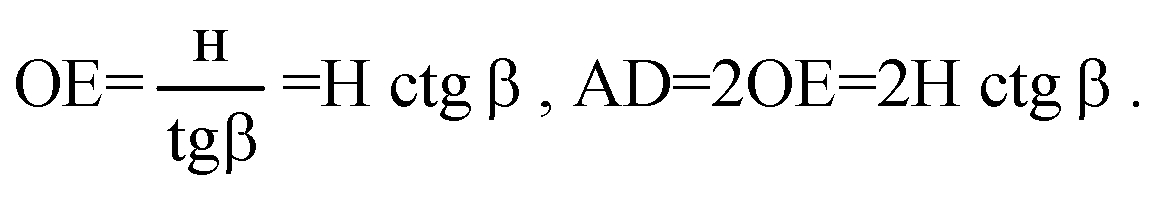
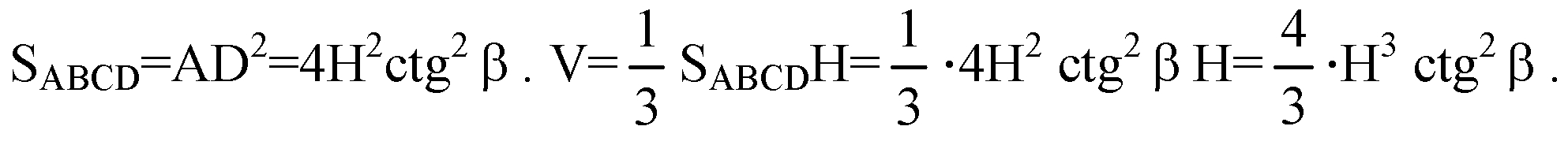
Б) SO — высота пирамиды. Проведем ОЕ перпендикулярно DC, отрезок SE. По теореме о трех перпендикулярах SE перпендикулярно DC.
В правильной пирамиде боковые ребра равны, ΔDSC — равнобедренный, высота SE — биссектриса и медиана.
Из треугольника ΔDSE:
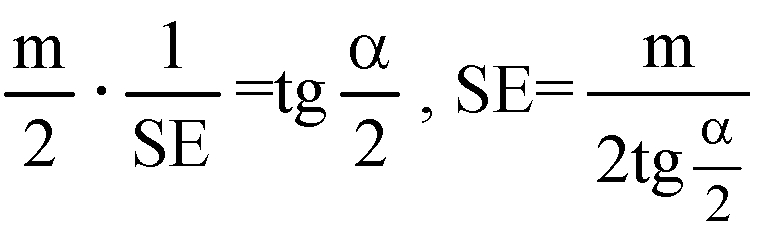
Из треугольника ΔSOE:
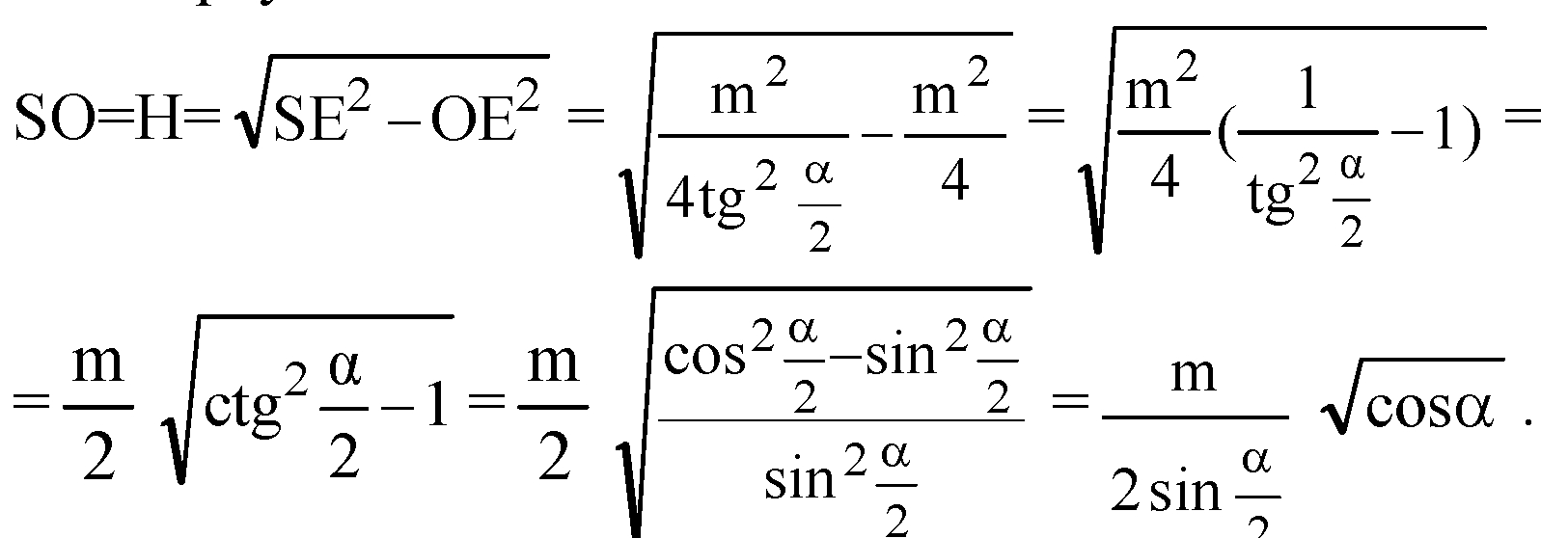
Площадь