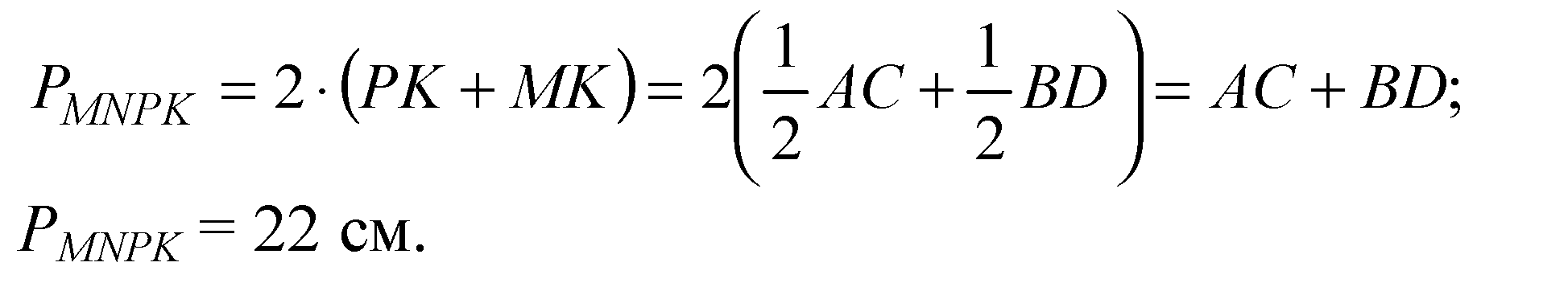Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 73
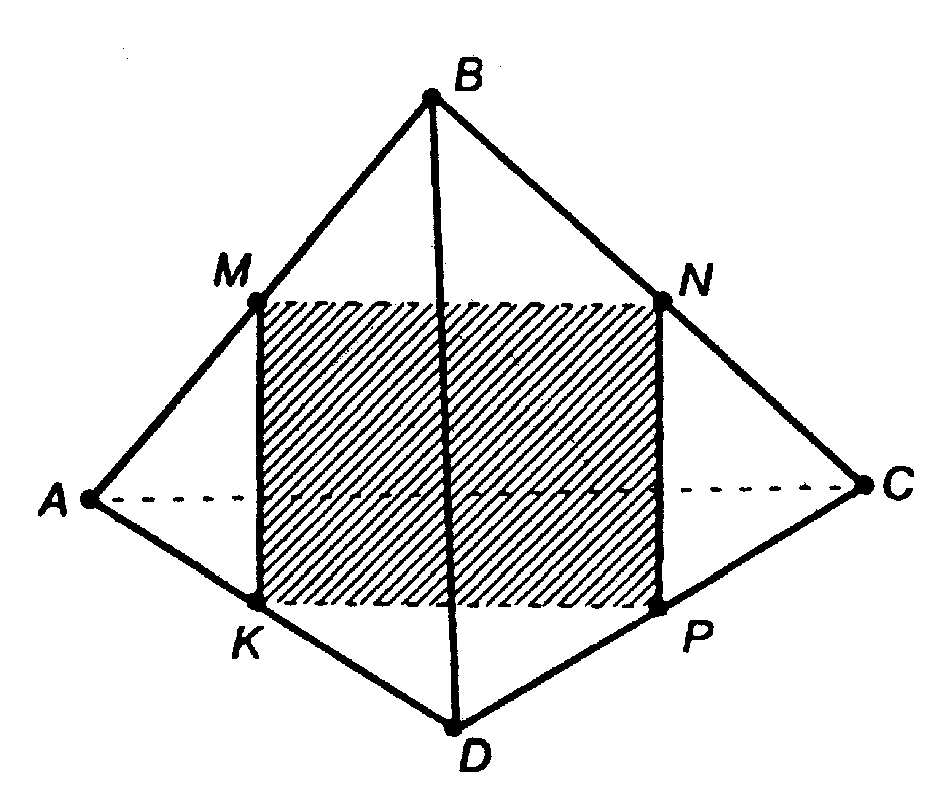
Найдем точки пересечения пл. MNP с ребрами тетраэдра.
NP — средняя линия
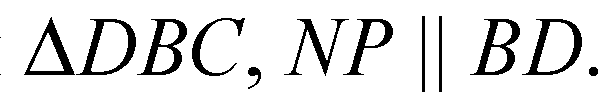
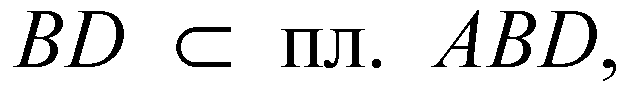
Поэтому
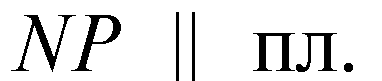
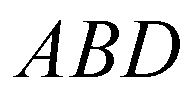
(теорема I).
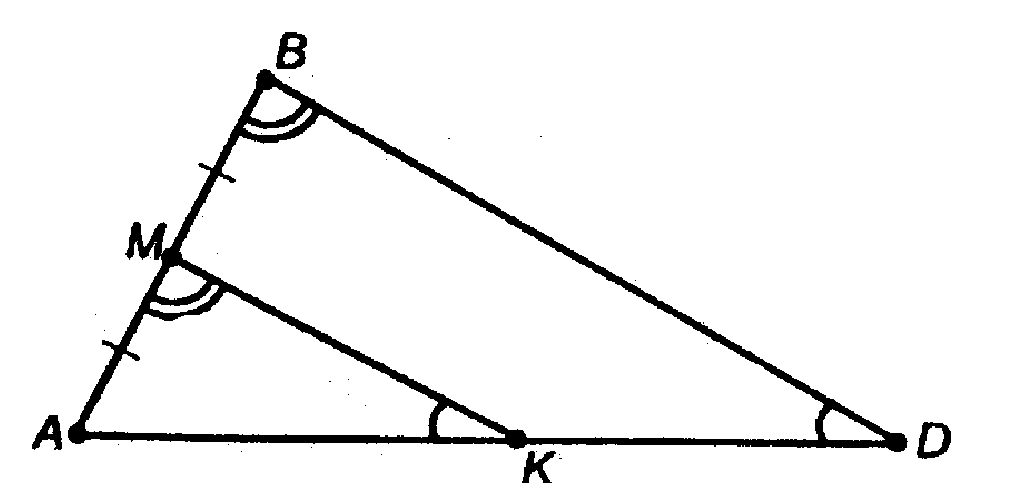
Плоскости ABD и MNP имеют общую точку М, значит они пересекаются по прямой, проходящей через т. М в пл. ABD.
Эта прямая параллельна NP, а раз
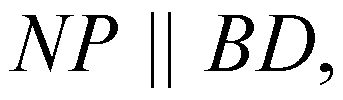
То эта прямая параллельна BD.
Пусть K — точка пересечения этой прямой с ребром AD (раз BD пересекает AD, тогда прямая, параллельная BD пересечет AD).
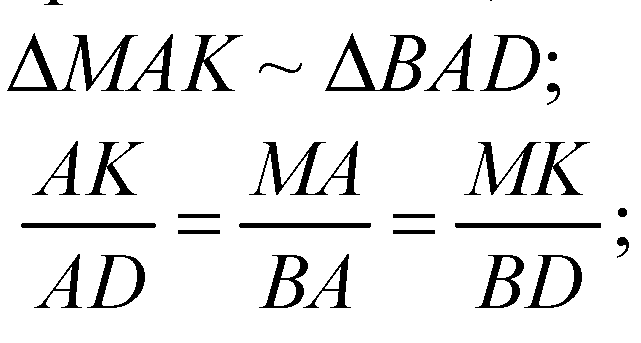
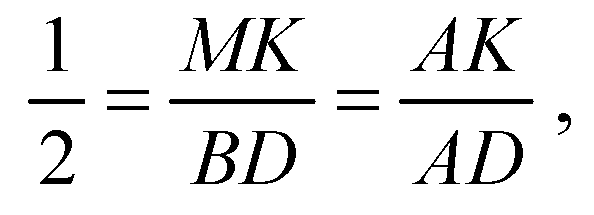
Поэтому точка K середина AD.
Утверждение доказано.
Аналогично получаем, что PK — средняя линия в ΔADC, поэтому
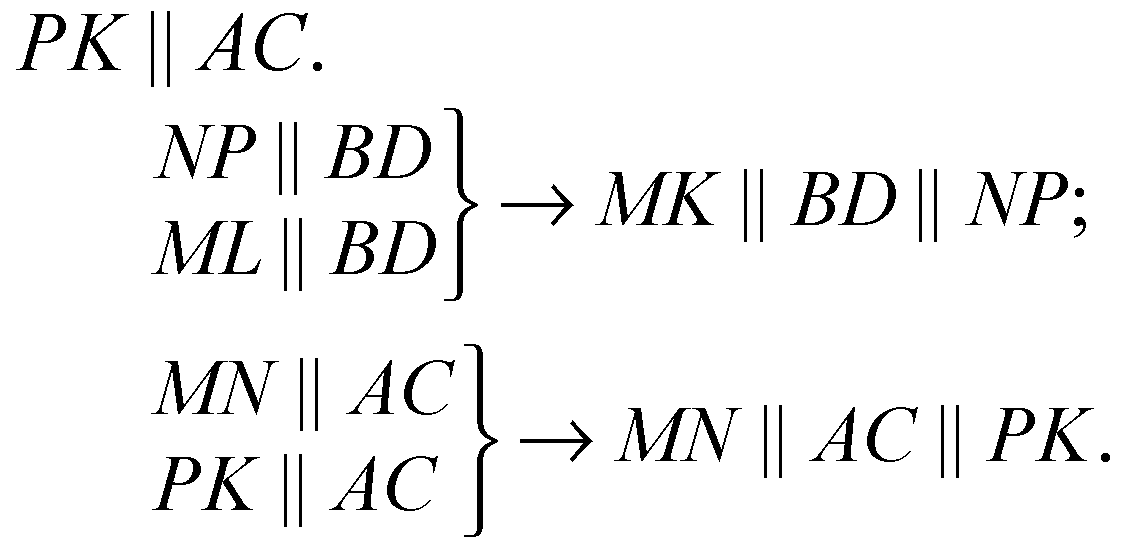
4-угольник MNPK — параллелограмм по определению.