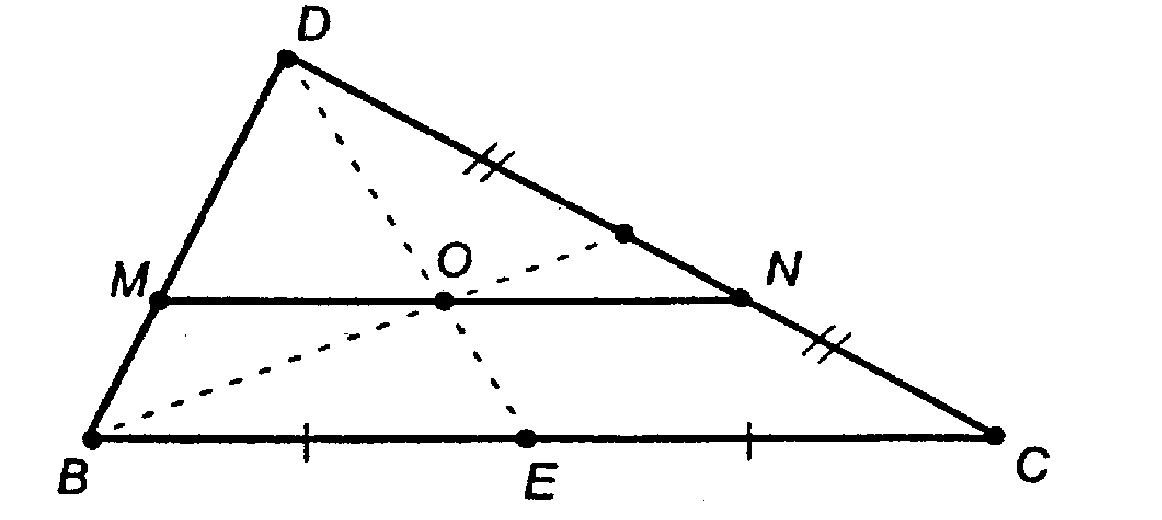
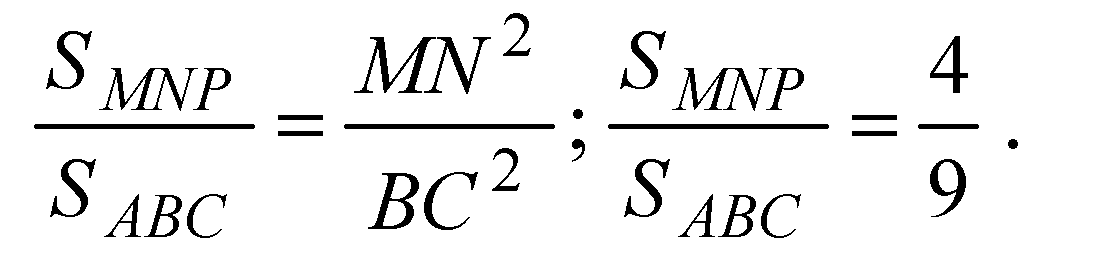Глава I Параллельность прямых и плоскостей. §4 Тетраэдр и параллелепипед. → номер 74 74. Через точку пересечения медиан грани BCD тетраэдра ABCD проведена плоскость, параллельная грани ABC. а) Докажите, что сечение тетраэдра этой плоскостью есть треугольник, подобный треугольнику ABC. б) Найдите отношение площадей сечения и треугольника ABC.
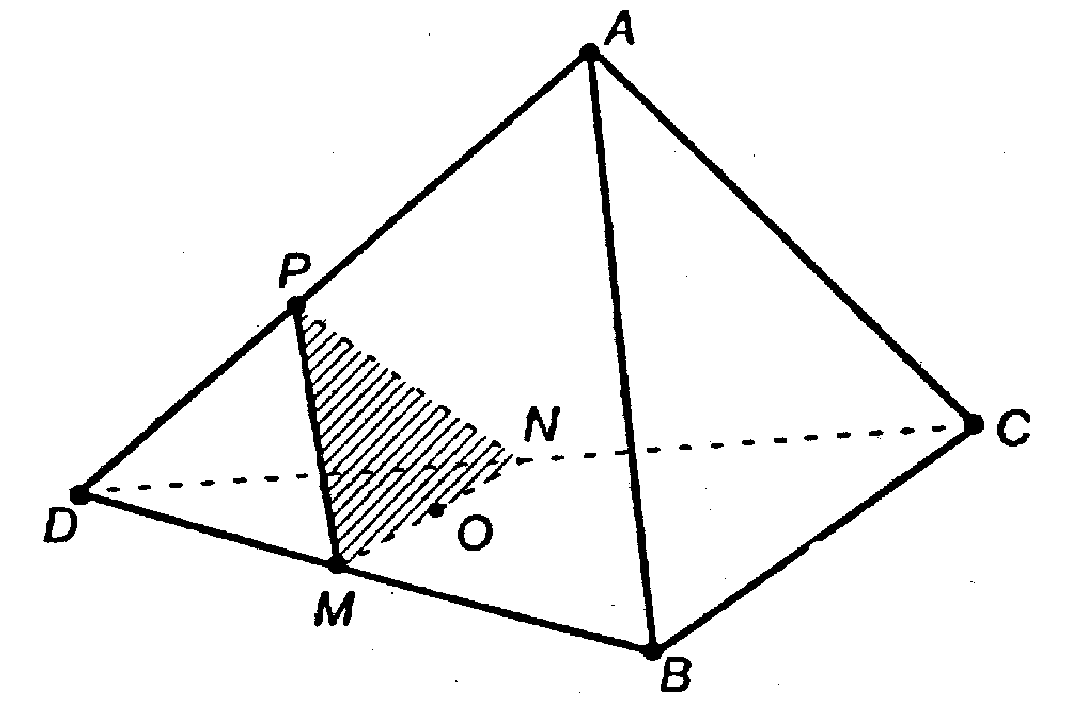
Пусть т. О — точка пересечения медиан ΔBCD.
Плоскость сечения имеет с гранью ADC общую т. N, значит, обе плоскости пересекаются по прямой, проходящей через т. N.
Плоскость сечения и параллельная ей пл. АВС пересекаются плоскостью ADC, значит линии пересечения параллельны,
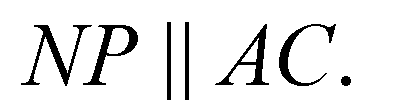
Аналогично,
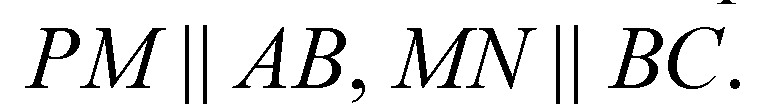
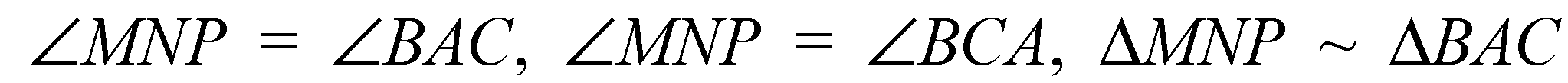
(по первому признаку).
Утверждение а) доказано. б)
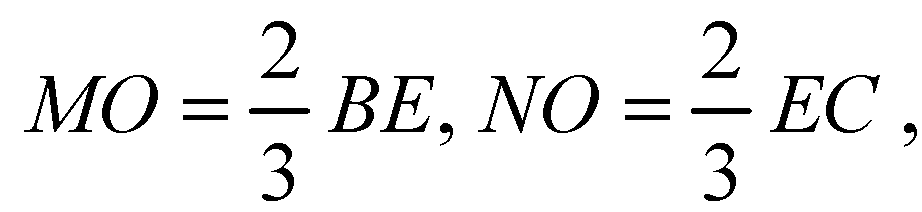
Потому что:
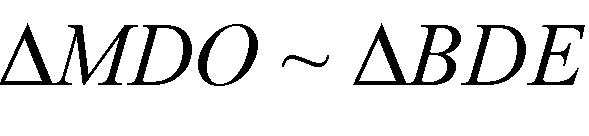
И
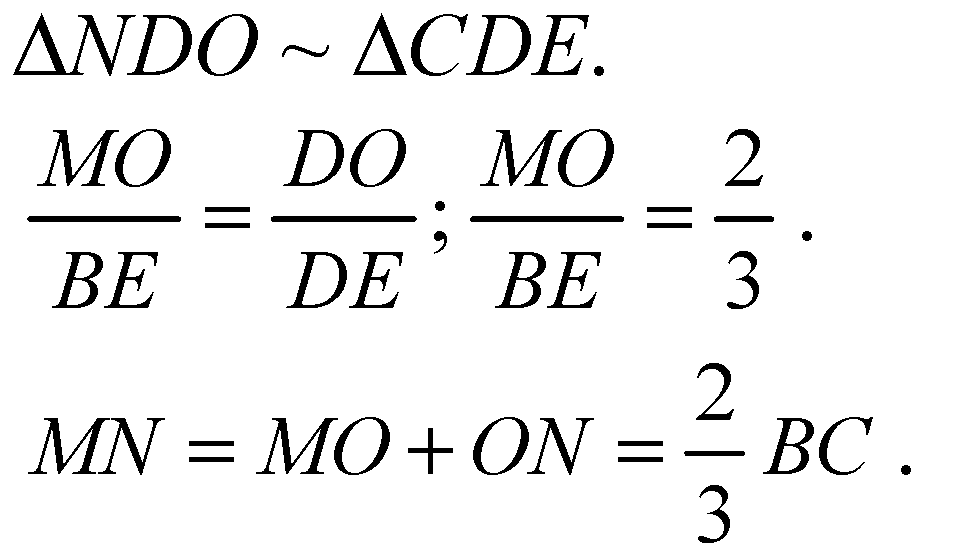
Отношение площадей подобных фигур равно отношению квадратов соответствующих линейных размеров.