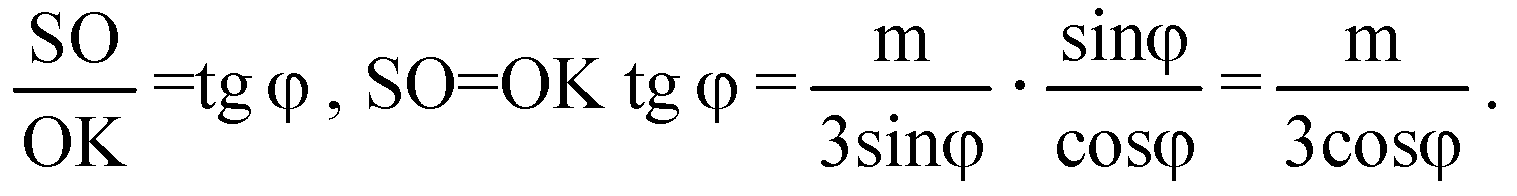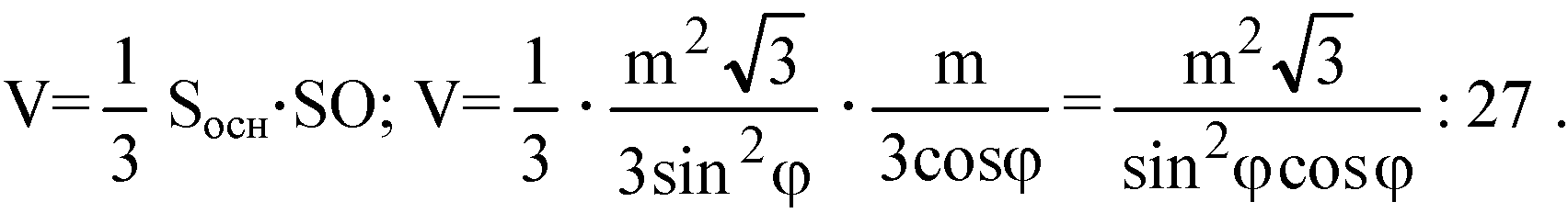Дополнительные задачи к главе VII → номер 736
Пусть SO — высота пирамиды, О — центр правильного ΔАВС. Проведем АК перпендикулярно ВС, отрезок SK. По теореме о трех перпендикулярах SK⊥BC, поэтому ∠AKS=φ — линейный угол двугранного угла при основании.
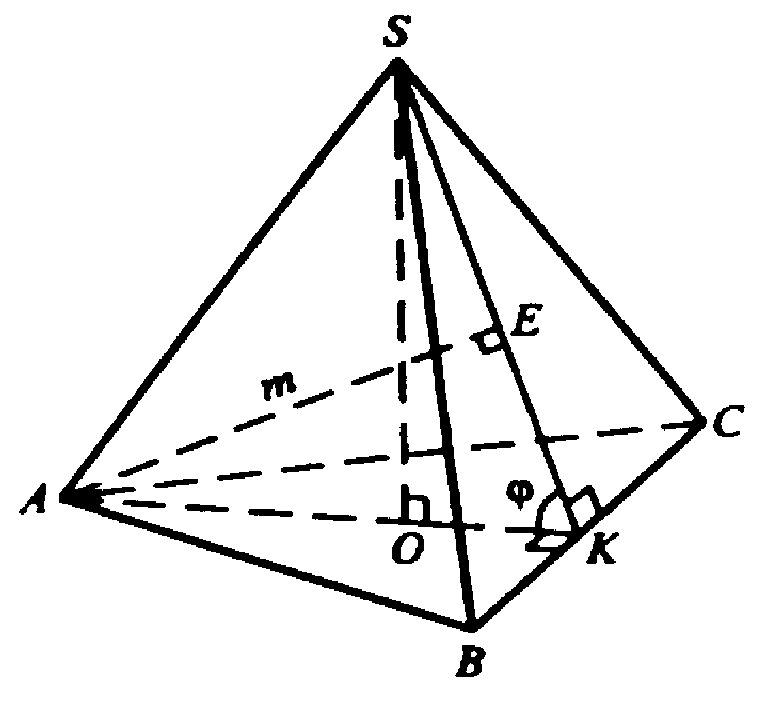
Проведем АЕ перпендикулярно плоскости BSC. Поскольку плоскость ASK перпендикулярна
Плоскости BSC, то АЕ ⊂ плоскости ASK.
Из прямоугольного ΔАЕК:
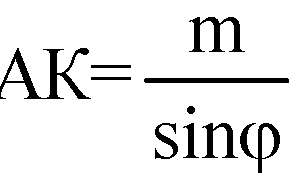
Обозначим сторону основания равной
Х, тогда из треугольника ΔАВК:
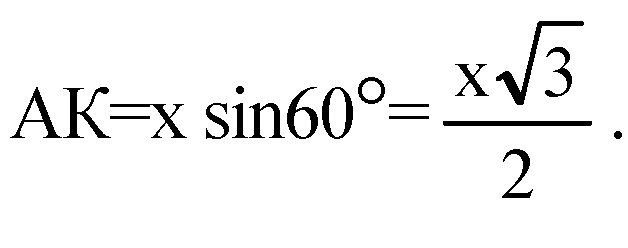
Тогда,
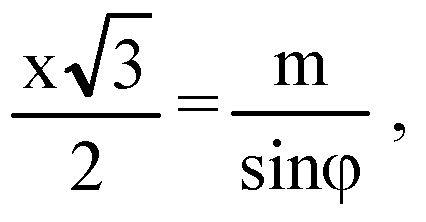
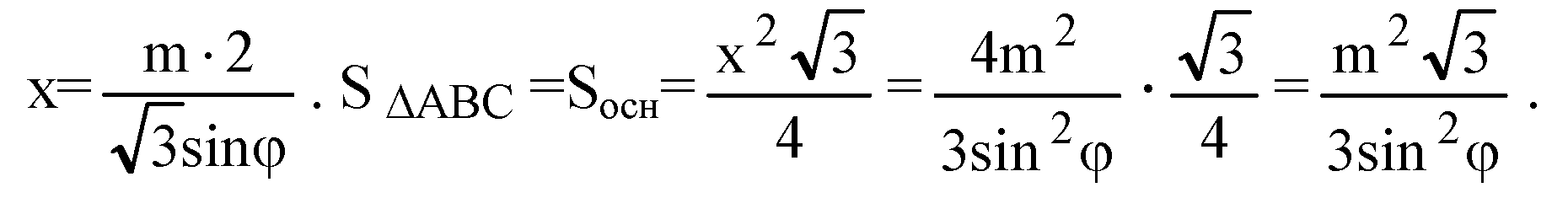
В ΔABC ОК — радиус вписанной окружности,
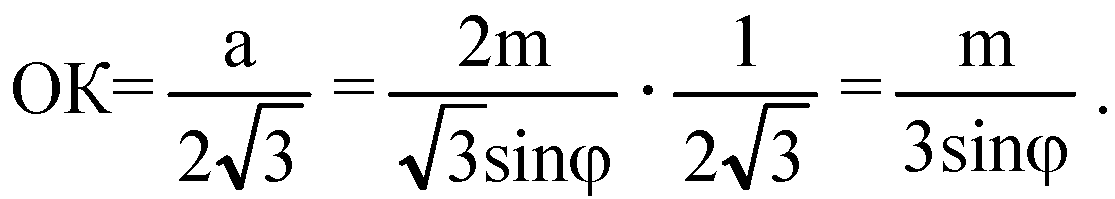
В ΔSOK: