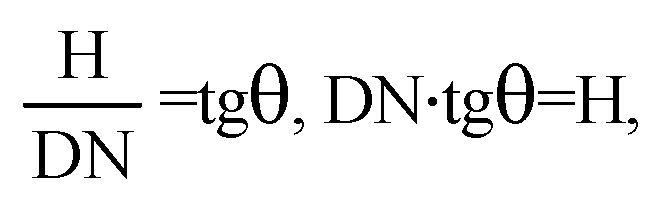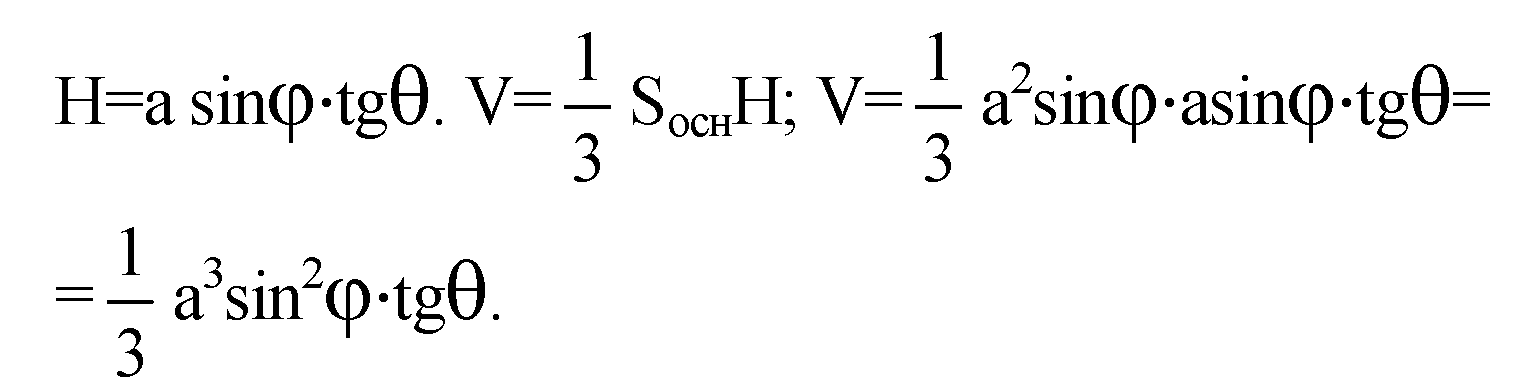Дополнительные задачи к главе VII → номер 742 742. Основанием пирамиды является ромб со стороной а. Две боковые грани пирамиды перпендикулярны к плоскости основания и образуют тупой двугранный угол φ. Две другие боковые грани составляют с плоскостью основания двугранные углы Θ. Найдите объем пирамиды.
Линия пересечения двух плоскостей, перпендикулярных к третьей плоскости — перпендикуляр к этой плоскости; значит, PD перпендикулярна
Плоскости ABCD. PD — высота пирамиды, PD=H. ∠ADC=φ — линейный
Угол двугранного угла при ребре PD. В основании ABCD ∠А=∠С=180°-φ.
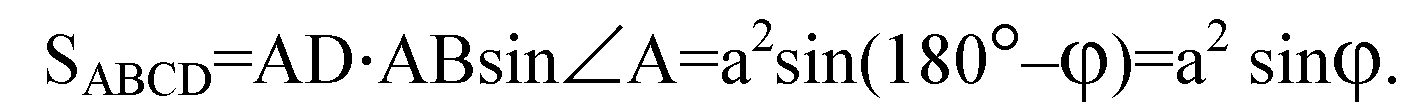
Построим DM⊥AB, DN⊥CB. По теореме о трех перпендикулярах отрезки РМ⊥АВ, PN⊥BC.
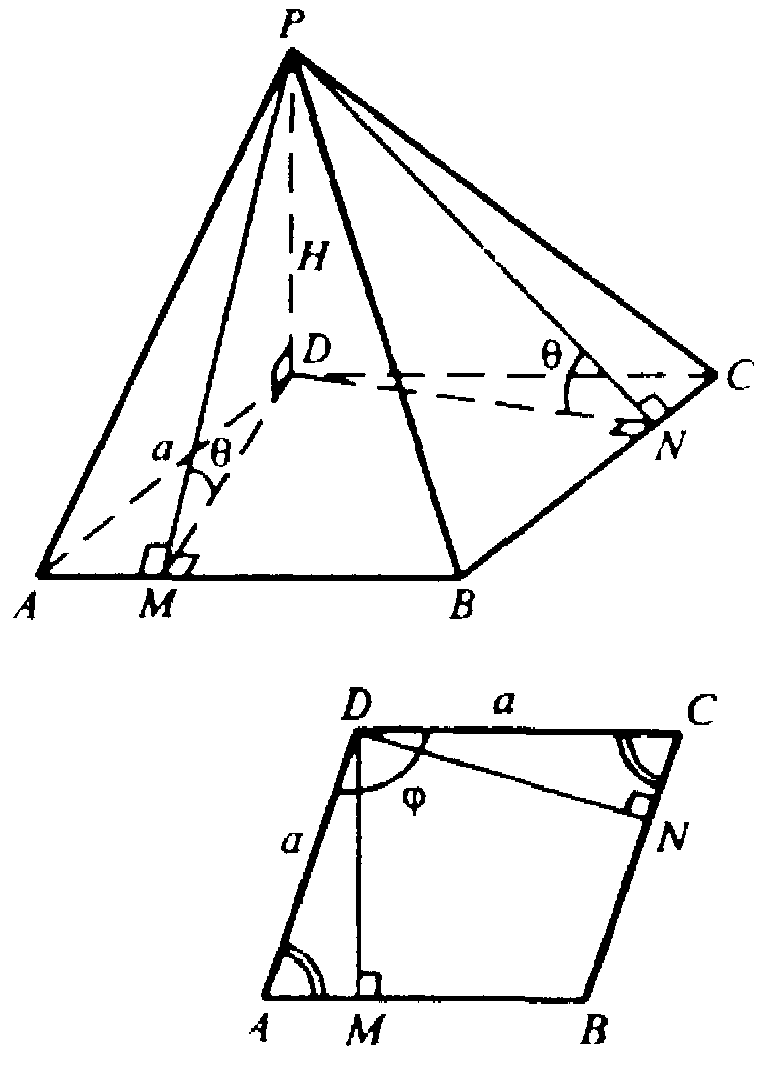
∠PMD=∠PND=Θ — линейные углы двугранных углов, образованных боковыми гранями РАВ и РВС с плоскостью основания.
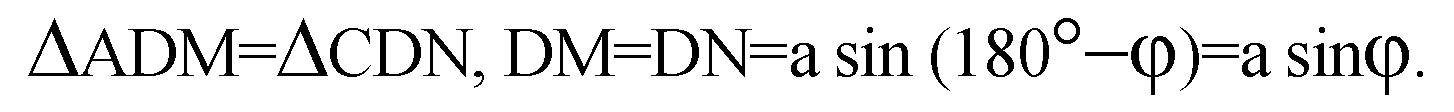
Из треугольника PDN: