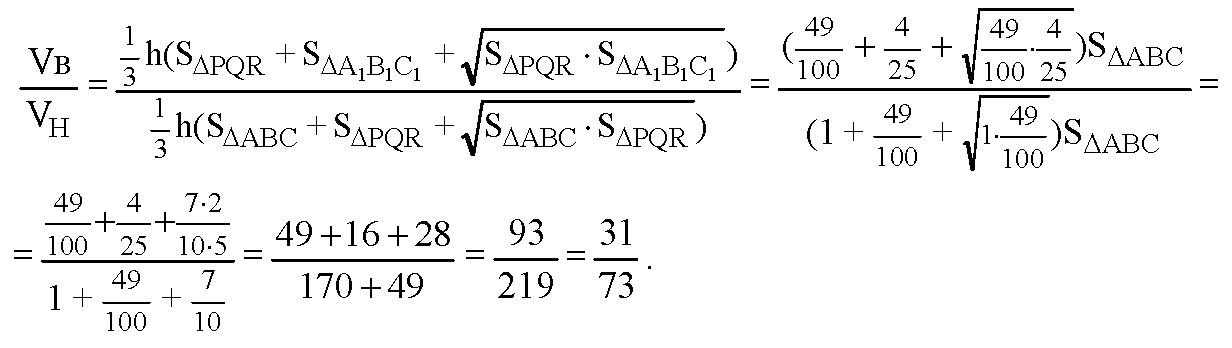Дополнительные задачи к главе VII → номер 744
Обозначим
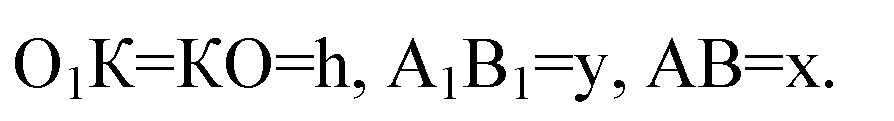
По условию
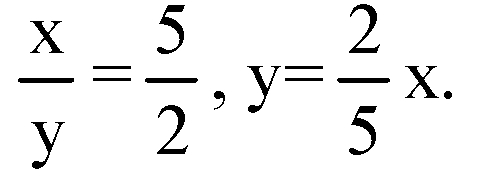
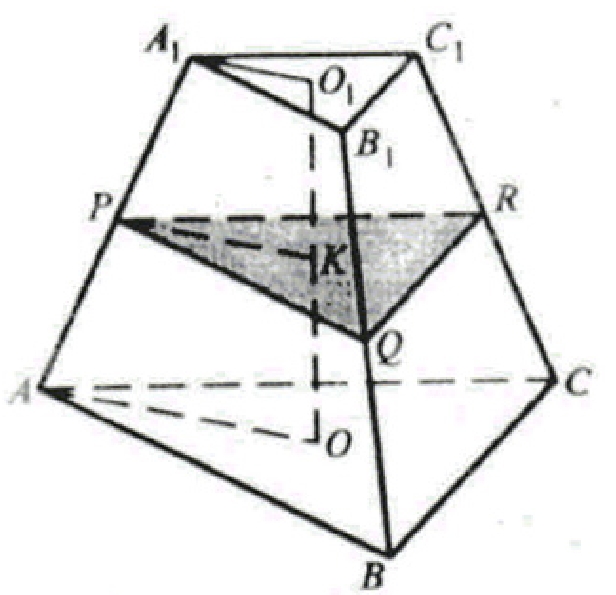
Рассмотрим трапецию АА1О1О. РК||АО, отрезок РК — средняя линия трапеции, значит, А1Р=РА.
Рассмотрим грань АА1В1В. Это трапеция, через точку Р проведен отрезок PQ||АВ, поэтому PQ является средней линией трапеции.
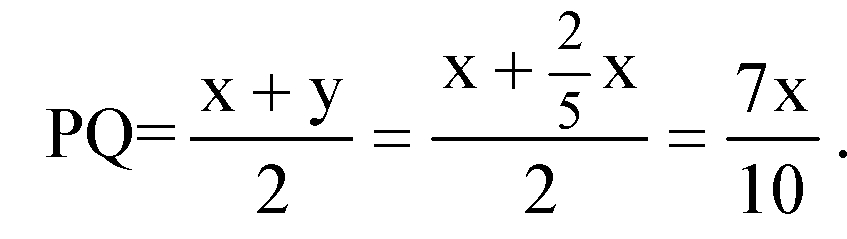
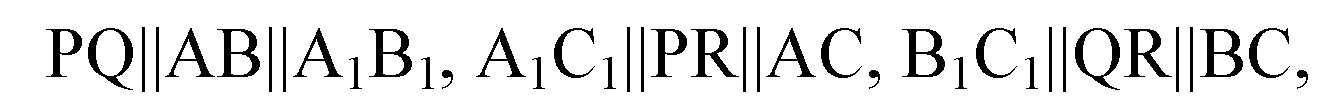
Тогда,
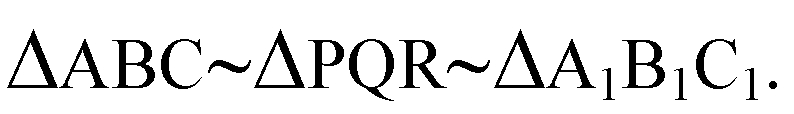
Площади подобных фигур относятся как квадраты их сходственных сторон.
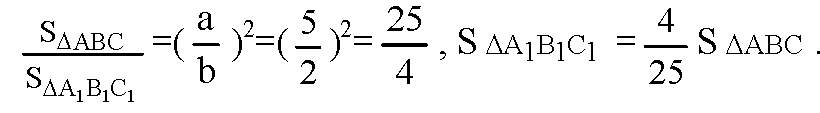
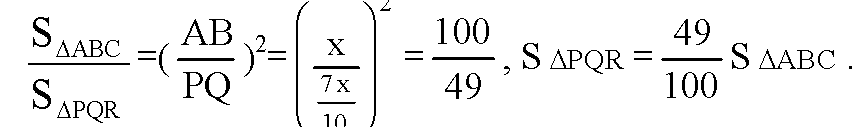
Обозначим объем верхней усеченной пирамиды VВ, а объем нижней усеченной пирамиды VН.
Тогда