Задачи повышенной трудности → номер 778
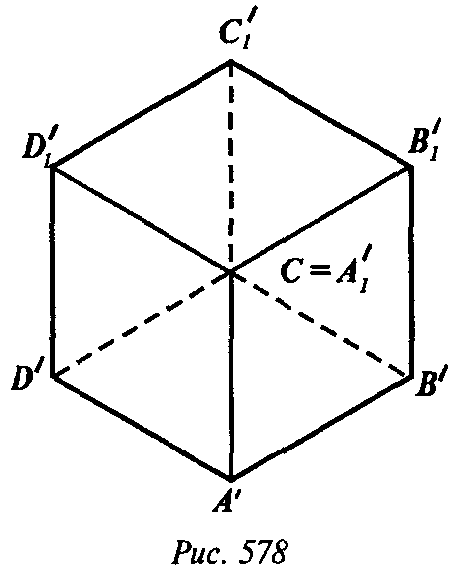
Проекция данного куба ABCDA1B1C1D1 на плоскость α, перпендикулярную его диагонали А1С, является правильным шестиугольником A’B’B1’C1’D1’D’. Ребра куба, исходящие из вершин А1 и С, образуют с α равные углы; обозначим их величины через φ.
В ΔAA1C
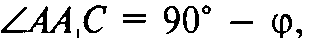
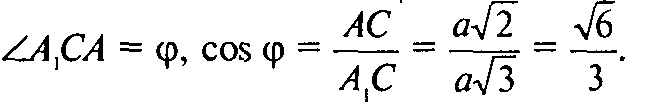
Все стороны полученного шестиугольника равны каждая
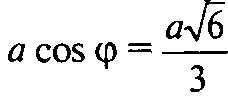
Радиус окружности, в него вписанной,
Равен
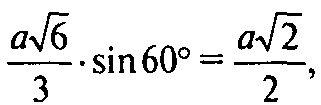
А сторона квадрата, вписанного в эту ок
Ружность, равна
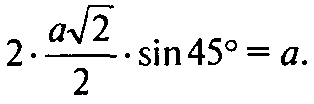
Этот квадрат лежит внутри этого шестиугольника. Поэтому через отверстие, направленное вдоль А1С и проецируещееся в этот квадрат, можно протащить куб с ребром а.
Если сторону этого вписанного в окружность квадрата провести параллельно А’В’ и продолжить его диагонали, то они пересекут стороны шестиугольника в вершинах квадрата, вписанного в этот шестиугольник и имеющего сторону, большую а. Через соответствующее отверстие можно протащить куб, больший данного.
