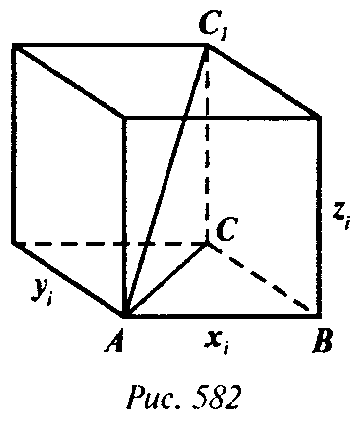
Задачи повышенной трудности → номер 783 783. Внутри куба с ребром 1 см расположена ломаная, причем любая плоскость, параллельная любой грани куба, пересекает ее не более чем в одной точке. Докажите, что длина ломаной меньше 3 см. Докажите также, что можно построить ломаную, обладающую указанным свойством, длина которой сколь угодно мало отличается от 3 см.
Пусть ui, — длина i-го отрезка ломаной, хi, уi, zi — длины его проекций на три ребра куба с общей вершиной. Согласно условию проекции отрезков не имеют общих точек, следовательно
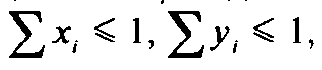
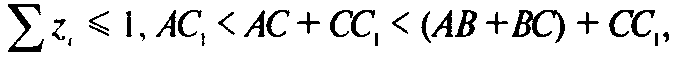
В соответствии с этим
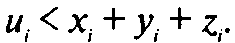
Отсюда
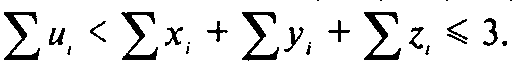
Пусть теперь куб на рисунке — данный, его ребро равно 1, и ломаная АВ0C0C лежит внутри куба. Если точки B0 и С0 достаточно близки к В и С, то длина этой ломаной сколь угодно близка к длине ломаной АВСС1, то есть к 3.
