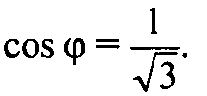Задачи повышенной трудности → номер 788 788. В правильном треугольнике ABC сторона равна а. На сонаправленных лучах BD и СЕ, перпендикулярных к плоскости ABC, взяты точки D и Е так, что BD=a/√2 , СЕ = а√2. Докажите, что треугольник ADE прямоугольный, и найдите угол между плоскостями ABC и ADE.
Пусть
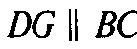
И
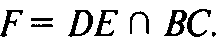
Тогда
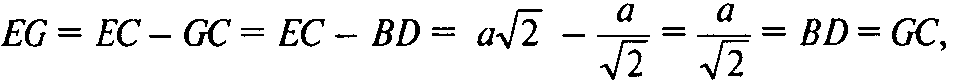
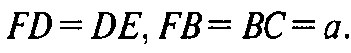
Из ΔABD:
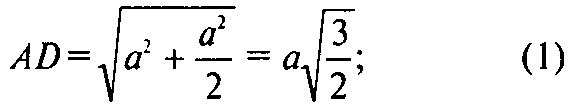
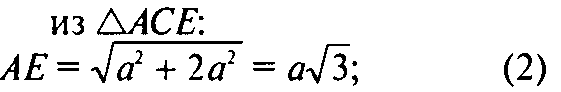
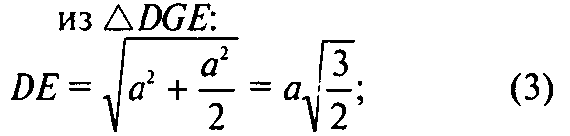
Из (1), (2), (3) и по теореме, обратной теореме Пифагора,
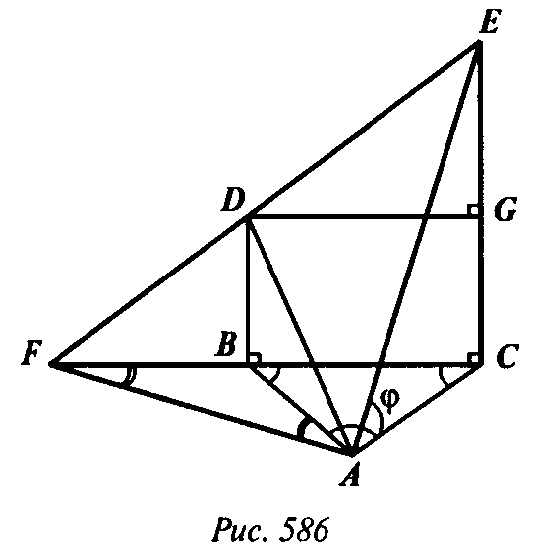
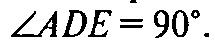
В ΔFBA:
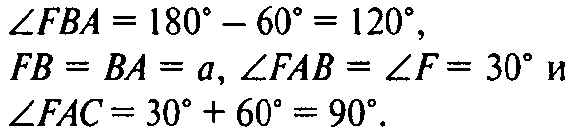
По теореме о трех перпендикулярах
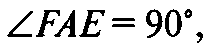
И
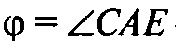
Искомый угол между плоскостями. Из ΔАСЕ