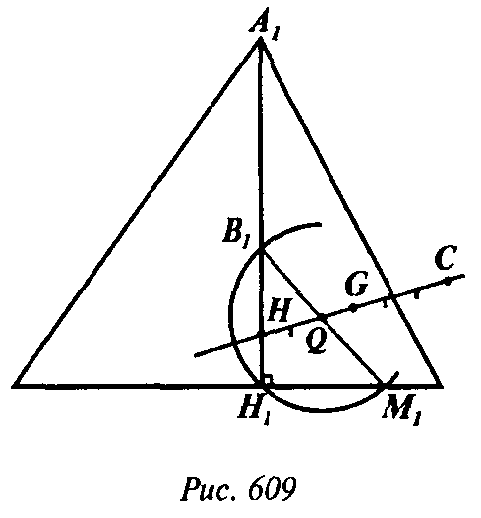
Задачи повышенной трудности → номер 815 815. Дан тетраэдр, все высоты которого пересекаются в одной точке. Докажите, что точки пересечения медиан всех граней, основания высот тетраэдра и точки, которые делят каждый из отрезков, соединяющих точку пересечения высот с вершинами, в отношении 2:1, считая от вершины, лежат на одной сфере, центр которой расположен на прямой Эйлера (сфера Эйлера).
Сохраним обозначения из №814. Докажем, что точка Q, для которой
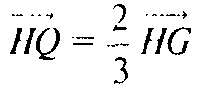
— центр сферы
Эйлера.
Если точка B1 делит отрезок AH в соотношении 2:1, то
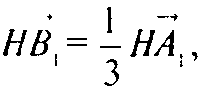
А если M1 — центроид грани A2A3A4, то согласно №366
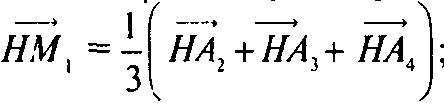
По лемме 2 из №814
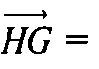
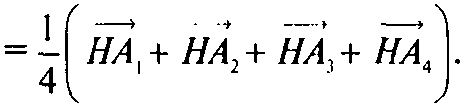
Отсюда
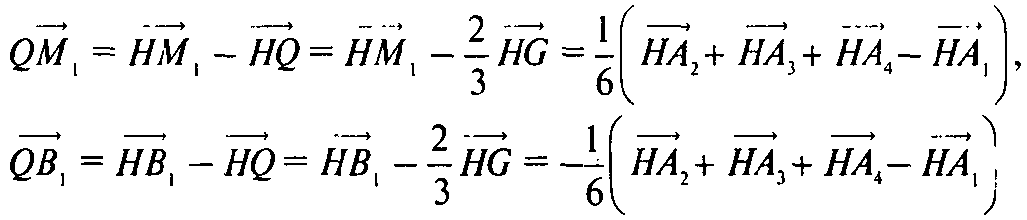
Аналогично находим остальные векторы
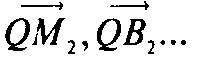
В №814 доказано, что все произведения
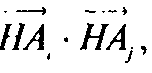
Где i, j = 1,2,
3, 4, i≠j, равны между собой. Поэтому после раскрытия скобок получим
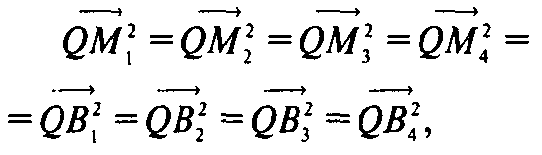
Следовательно, все точки Мi и Bi лежат на сфере с центром Q.
Так как
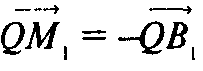
То М1 и В1 — концы диаметра этой сферы; так как В1 и H лежат на высоте A1H1, а H1 и М1 — на перпендикулярной ей грани А2А3А4 то В1Н1М1 и H1 лежит на сфере. Аналогично на сфере лежат и точки H2, H3, H4.
