Задачи на построение → номер 355
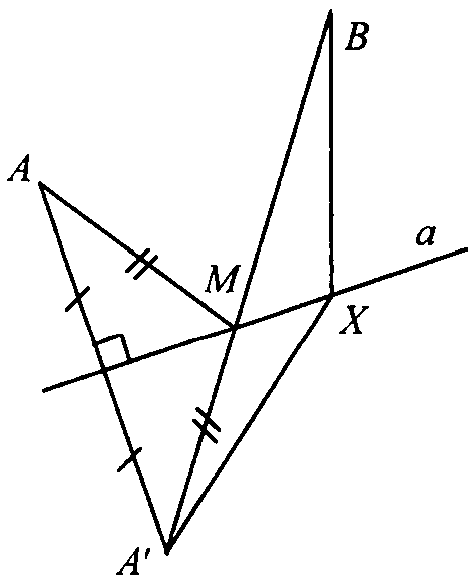
Из точки А опускаем перпендикуляр на а. Пусть К — точка пересечения. С другой стороны прямой откладываем точку А’ с условием АК = А’А. Соединяем точки А’ и В.
Пусть М — пересечение А’В и пр. а. М — искомая точка, поскольку выполняется неравенство треугольника:
АМ+ МВ = А’М+ MB (т. к. ΔАА’М — равнобедренный) = А’В < АХ + ХВ.