Упражнение 2 → номер 1 № 1. Группа туристов, двигаясь с постоянной по модулю скоростью 5 км/ч, сначала в течение 1 ч идет на север, затем в течение 0,5 ч — на восток и, наконец, в течение 1,5 ч — на юг. Где окажется группа после прохождения этих трех участков? Сколько времени ей потребуется на возвращение в исходную точку по прямой?
За начало отсчета координат примем точку отправления группы туристов. Оси координат направим вдоль сторон света.
На рис. 1 изобразим траекторию движения туристов. Весь путь разобьем на четыре участка, на которых движение группы определяете: векторами перемещения S1,S2,S3,S4 соответственно в направлении на север, восток, юг и обратно в исходную точку. На каждом из них укажем скорость движения V и отметим время движения t1, t2,
T3, t4.
Дано:
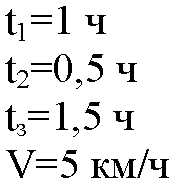
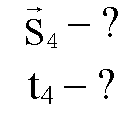
Решение:
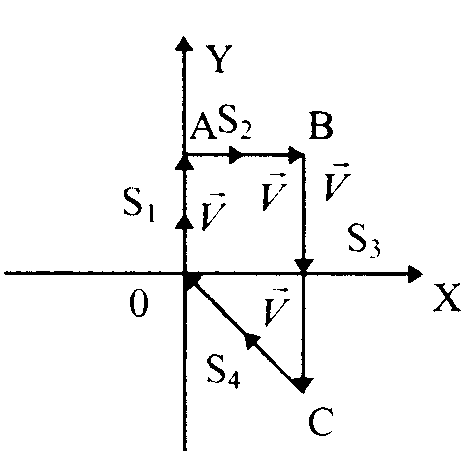
Определим длину перемещения группы на участках ОА; АВ; ВС:
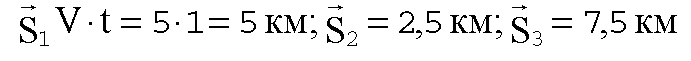
Определим координаты группы в (⋅) А:
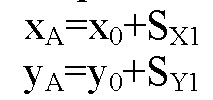
Т. к. S направлен вдоль оси Y, следовательно
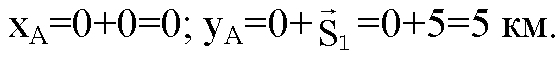
Координаты группы, в (⋅) В:
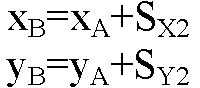
Т. к. S2 направлен вдоль оси X, следовательно
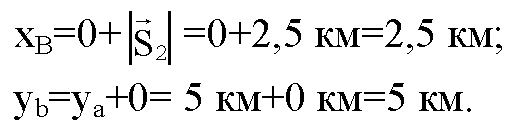
Аналогичным путем определяем координаты группы в точке С:
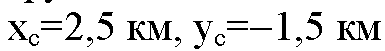
Длину вектора S4 определим по теореме Пифагора:
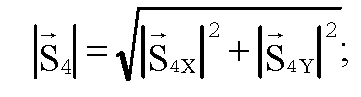
Т. к.
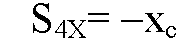
И
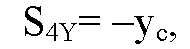
То
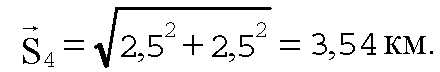
Т. к. точка С находится в IV четверти координатной плоскости и лежит на прямой являющейся биссектрисой угла YOX (т. к. |уС| = |yC|),
То можно сделать вывод, что преодолев три участка ОА, АВ, ВС, группа оказалась на расстоянии 3,5 км к юго-востоку от исходного пункта. Время, требуемое на возвращение в исходную точку по прямой:
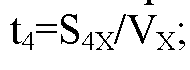
По теореме
Пифагора
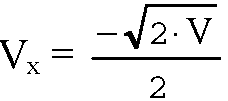
Отсюда
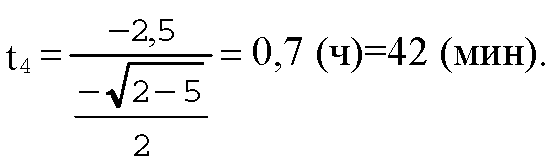
Ответ: 42 мин.
