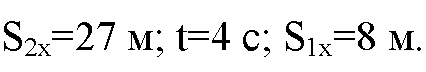Упражнение 7 → номер 1 № 1. Постройте в координатных осях (х, t) графики скорости двух тел, движущихся равноускоренно: одно с возрастающей по модулю скоростью, другое — с убывающей. Начальные скорости и ускорения тел соответственно равны: 1 м/с и 0,5 м/с2; 9 м/с и 1,5 м/с2. Какой путь пройдет второе тело до остановки? Через какое время скорости обоих тел станут одинаковыми и какой путь пройдет за это время первое тело?
Дано
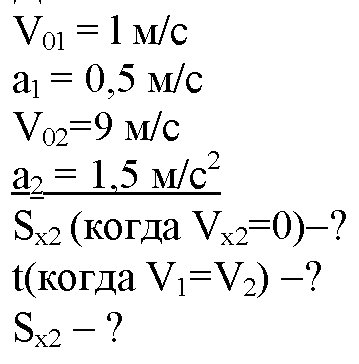
Решение:
Построим графики скорости в координатных для первого и второго тела. Примем за начало времени момент, когда тела стали двигаться со скоростями V01 и V02.
Т. к. графики скорости при равноускоренном движении — прямые линии, то достаточно двух точек для построения графиков скорости. Первые точки у нас уже есть.
Для первого тела: А(1 м/с, 0).
Для второго тела: В(9 м/с, 0).
Для вычисления вторых точек воспользуемся формулой для определения скорости при равноускоренном движении в момент времени t:
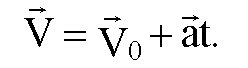
Приняв направление движения двух тел вдоль оси Х мы можем записать векторное уравнение для определения скорости в проекциях на ось X:
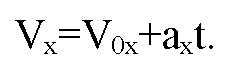
Для первого тела: т. к. движение ускоренное: ax=a1; V0x=V01. Пусть. t=1c, тогда:
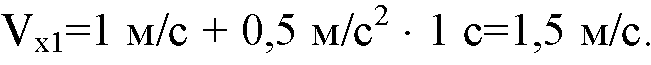
На координатной плоскости обозначим эту точку за A1.
Для второго тела: т. к. движение замедленное:
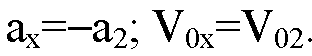
Пусть t=1c, тогда:
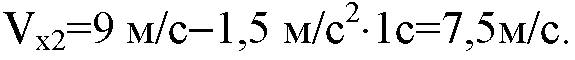
На координатной плоскости обозначим эту точку за B1. Теперь проводя прямые через точки А и A1; В и В1 соответственно получим графики скоростей для первого тела и для второго (I — для первого тела, II — для второго тела):
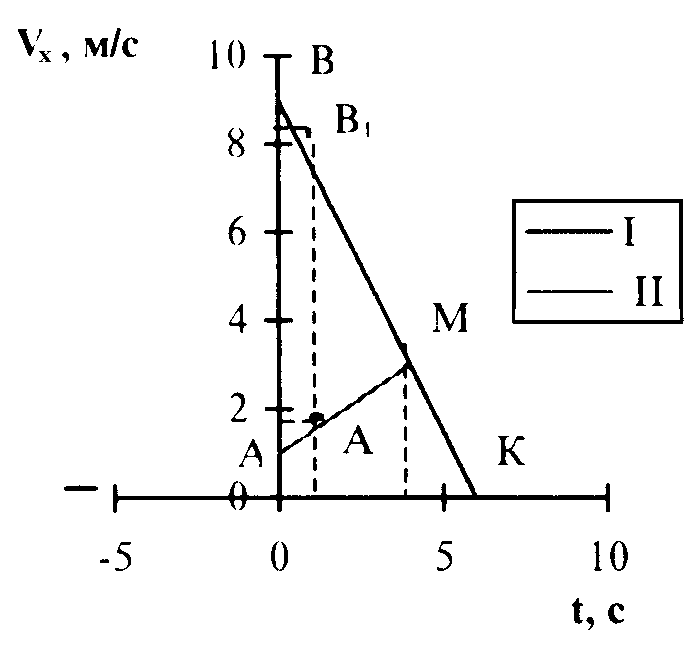
(⋅) К соответствует значению времени, когда второе тело остановится. (⋅) М — точка равенства скоростей I-го и II-го тел.
Момент времени, когда II-ое тело остановится, найдем из формулы для определения скорости при равноускоренном движении:
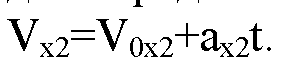
Т. к. движение замедленное, то ах2=—а2; Vx2=0. Подставляя, получим:
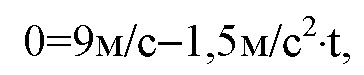
Отсюда:
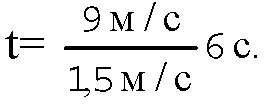
Путь за это время t определим по формуле для равноускоренного движения II-ого тела:
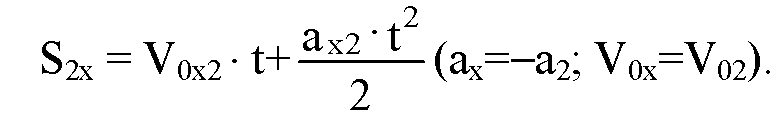
Итак,
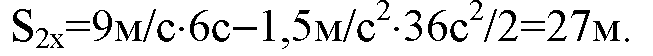
Скорости обоих тел будут одинаковыми в (⋅)М на координатной плоскости (Vx, t). Скорость в ()М для первого тела определяется по формуле:
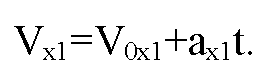
В нашей задаче:
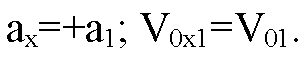
Скорость в ()М для второго тела определяется по формуле:
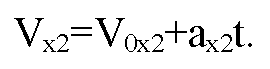
В нашей задаче:
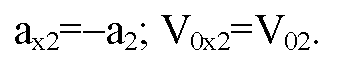
Приравнивая друг другу значения Vx1 и Vx2 и решая полученное уравнение относительно времени t, получим:
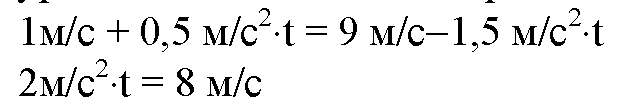
T = 4c — за это время скорости первого и второго тел сравняются. Путь пройденный первым телом за это время определим по формуле:
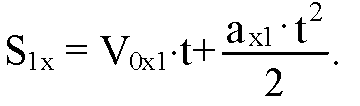
В нашей задаче:
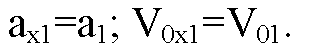
Итак,
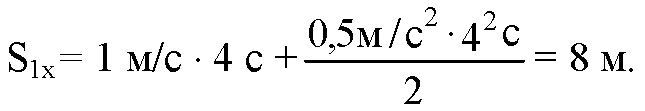
Ответ: