На потолке в углу С комнаты (рис. 173) сидит паук, а на полу в противоположном углу К спит муха. Какой путь должен избрать паук, чтобы добраться до мухи по кратчайшему расстоянию?
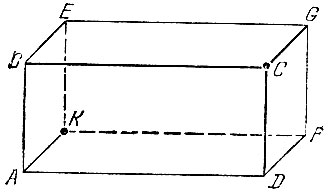
Рис. 173
Решение. С первого взгляда кажется ясным, что паук должен пробежать потолок по диагонали СЕ и затем спуститься к мухе по ребру ЕК.
Поразмыслив, мы найдем для паука и другой путь: он может пробежать боковую стену по диагонали CF и подобраться к жертве по FK.
И, наконец, паук мог бы пойти по СА и по АК.
Параллелепипед симметричен относительно середины диагонали СК, поэтому каждый из путей CDK, СВК, и CGK равен по длине одному из трех приведенных выше путей.
Какой же из них является кратчайшим?
Оказывается, что ни тот, ни другой, ни третий. Есть еще более короткие пути, займемся их разысканием.
Ввиду симметрии параллелепипеда можно считать, что кратчайший путь паука не заходит на боковую стену АВЕК. Действительно (рис. 174), например, длина пути KLC равняется длине пути КМС. Поэтому можно считать, что путь пересекает одно из ребер EG, GF, FD, AD. Ввиду симметрии ребер AD и EG доста^ точно считать, что он пересекает EG, GF или FD.
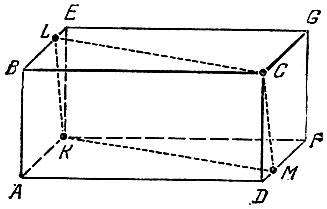
Рис. 174
Развернем параллелепипед, изображающий нашу комнату, на плоскость. Получим чертеж, представленный на рис. 175.
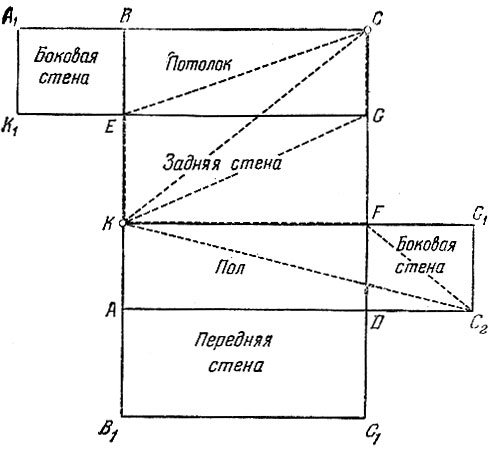
Рис. 175
Паук сидит в точке С, а муха — в точке К. Теперь мы ясно видим, что пути СЕК и CGK, казавшиеся нам в неразвернутом чертеже кратчайшими, на самом деле таковыми не являются. Стоит соединить точки С и К прямой линией, чтобы получить заметно более короткий путь. Этот путь будет кратчайшим среди всех путей, пересекающих ребро EG. Аналогично, путь КС2 будет кратчайшим среди всех путей, пересекающих ребро FD (точка С2 также отвечает вершине С нашего параллелепипеда). В частности, он будет короче пути CFK.
Для того чтобы представить себе кратчайший среди путей, пересекающих ребро GF, развернем комнату, как показано на рис. 176. Мы видим, что КС3 — кратчайший из путей, пересекающих ребро GF.
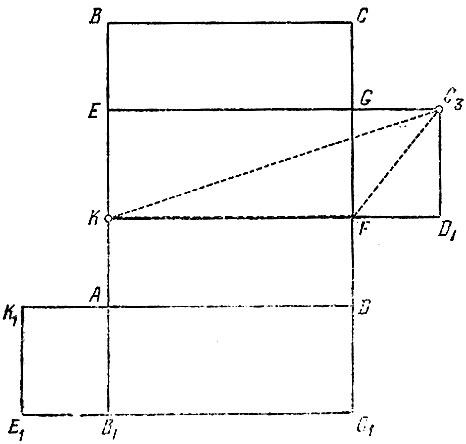
Рис. 176
Остается теперь решить вопрос: какой же из этих трех путей (КС, КС2, КС3) будет самым коротким. Сказывается, что это зависит от относительных размеров комнаты в длину, ширину и высоту.
Обозначим длину комнаты AD через а, высоту АВ через b и ширину А К через с. Тогда из рис. 175 и 176 имеем
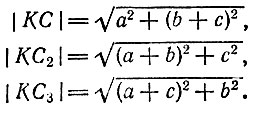
Раскрывая скобки и сравнивая между собой подкоренные выражения, мы видим, что они отличаются друг от друга лишь членами 2bc, 2ab, 2ас. Деля все три произведения на 2abc, получим 1/a, 1/b, 1/c. Отсюда видно, что если а > b, a > с, то кратчайшим путем будет путь КС; если с > а, с > b, то кратчайший путь KС2; если же b > a, b > с, то кратчайший путь КС3.
Мы видим, что кратчайший путь паука должен пересекать самое длинное из ребер EG, GF, FD.
Задача о пауке и мухе оказалась гораздо сложнее, чем можно было думать с первого взгляда.
Мосты и острова
Не приходилось ли вам жить, а может быть, вы и сейчас живете в городе или местности, где течет река, которая делится на протоки и рукава, образующие острова? Через реку и ее протоки переброшены, быть может, мосты, соединяющие различные части города. В Ленинграде, например, очень много подобных протоков, разветвлений Невы и разных каналов, через которые переброшено весьма большое количество мостов и переходов. Не приходила ли вам когда-нибудь в голову мысль (если, конечно, вы живете в местности, где есть река, острова и мосты) совершить такую прогулку, чтобы во время ее перейти все эти мосты, но перейти их так, чтобы на каждом побывать только по одному разу? Вряд ли вы думали об этом, а между тем мы стоим здесь перед весьма интересной и важной задачей, поставленной впервые знаменитым математиком Эйлером. Она служит отличным введением в совсем особую область геометрии, которую можно было бы назвать геометрией расположений.
Геометрия расположений занимается только вопросами порядка и расположения, оставляя в стороне все относящиеся к измерению и отношению величин геометрических фигур и тел. Все почти вопросы, связанные с такими играми, как шахматы, шашки, домино, лото, многие карточные задачи и т. д., наконец, такая практическая задача, как подбор разноцветных нитей для составления известного узора ткани,- все это относится к геометрии расположений. Значит, практически геометрия эта известна людям с глубокой древности. А на желательность ее научного развития указывал еще Лейбниц в 1710 году. Эйлер, как упомянуто, тоже занимался вопросами этого порядка, и, между прочим, задачей о мостах, которую мы здесь и излагаем в упрощенном виде.
Кроме того, поучительная сторона предлагаемых задач состоит в исследовании, возможна или нет данная задеча, прежде чем приниматься за решение ее. Эйлер, в частности, подробно исследовал случай невозможности.
