В шахматном матче встречаются две команды, состоящие из четырех человек. Каждый участник должен сыграть по одной партии с каждым игроком противной команды. Требуется составить расписание турнира так, чтобы:
1) каждый шахматист сыграл две партии белыми и две партии черными фигурами;
2) в каждом туре обе команды играли две партии белыми и две черными фигурами.
Решение. Рассмотрим квадрат из 16 клеток. Пусть его строки отвечают участникам первой команды, а столбцы — участникам второй команды.
Разместим в клетках квадрата пары цифр следующим образом. Возьмем размещение букв и цифр предыдущей задачи и заменим каждую букву соответствующей ей цифрой (П→1, М→2, К→3, Л→4). В результате получим рис. 171.
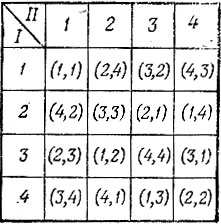
Рис. 171
Положим теперь, что первая цифра в каждой клетке указывает номер тура, в котором встречаются игроки, соответствующие строке и столбцу, содержащим данную клетку. И если вторая цифра нечетная, то игрок первой команды играет белыми, а в противном случае черными фигурами. Поскольку любая цифра, стоящая на первом месте, встречается в каждой строке и в каждом столбце по одному разу, то в любом туре будут заняты все шахматисты, при этом у каждого будет определен единственный партнер.
Покажем, что такое расписание удовлетворяет условиям задачи. Так как в каждой строке и в каждом столбце на втором месте расположены числа 1, 2, 3,4 в некотором порядке, то каждый шахматист сыграет по две партии белыми и по две партии черными фигурами. Далее, так как все пары различны, то, выбрав любые четыре пары чисел, отвечающие одному туру, т. е. имеющие на первом месте одну и ту же цифру — номер тура, мы получим на вторых местах расположенные в некотором порядке числа 1, 2, 3, 4. Это означает, что в данном туре игроки первой команды будут играть две партии белыми и две партии черными фигурами. Нагляднее это расписание игр представлено на рис. 172. Здесь цвет клетки означает цвет фигур, которыми должен играть представитель первой команды, а цифра — номер тура, в котором встречаются соперники.
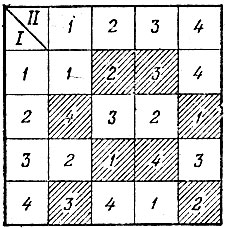
Рис. 172
Можно предлагать задачи, подобные двум последним, для любого числа п офицеров и полков и для команд с любым числом участников. Легко видеть, что при n = 2 первая задача неразрешима. Невозможно разместить четырех офицеров двух званий из двух полков так, как требуется в условии этой задачи. В 1782 году Эйлер предположил, что задача неразрешима при n = 2, 6, 10, 14, …, т. е. при всех n, которые при делении на 4 дают в остатке 2. Это было подтверждено в 1900 году для n = 6. И, наконец, в 1959 году было установлено, что при всех n ≠ 2, 6 задачу решить можно. Оказалось, что при n > 6 предположение Эйлера неверно. Он ошибся.
Пары латинских квадратов, решающие задачу 164 при некотором n, дают возможность составить расписание турнира с n участниками подобно тому, как это делалось в решении задачи 165. Интересно, что при n = 6 расписание турнира может быть составлено, хотя задача 164 неразрешима.
Заметим, наконец, что задачи этой главы представляют примеры вопросов, относящихся к разделу математики, называемому комбинаторикой.
