Возьмем 8 деревянных или из толстого картона кружков уменьшающегося диаметра и 3 вертикально укрепленные на подставках палочки (стержня). Кружки снабжены в центре отверстиями, и их накладывают, начиная с наибольшего, на одну из палочек А. Это и есть детская пирамида в 8 этажей (рис. 118, вверху).
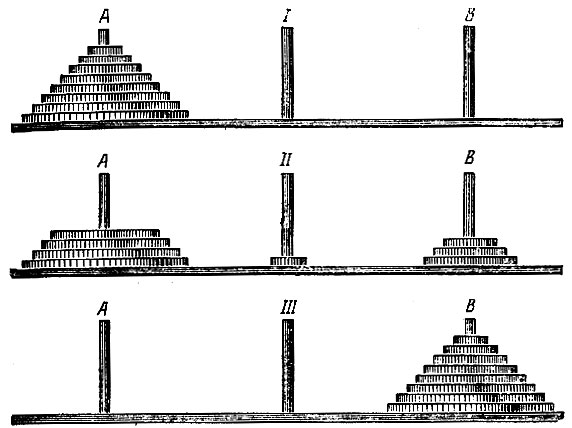
Рис. 118
Требуется эту пирамиду с палочки А перенести на палочку В, пользуясь третьей палочкой (I, II и III на нашем рисунке) как вспомогательной и соблюдая следующие условия: 1) не переносить за один раз более одного кружка, 2) класть снятый кружок или на ту палочку, которая свободна, или накладывать его на кружок большего диаметра. Надевать на какую-либо из палочек больший кружок поверх меньшего нельзя.
Решение. Чтобы показать процесс правильного перенесения кружков, обозначим кружки цифрами 1, 2, 3, …, 7, 8, начиная с наименьшего, затем изобразим процесс перенесения таблицей:

Отсюда мы видим, что на палочку III, когда она свободна, надеваются только нечетные кружки (1-й, 3-й, 5-й и пр.), а на В — только четные. Так что, например, для перенесения четырех верхних кружков нужно было сначала перенести три верхних на вспомогательную палочку — что, как видно из таблицы, потребовало семи отдельных перекладываний,- затем мы перенесли 4-й кружок на третью палочку — еще одно перекладывание — и, наконец, три верхних кружка со второй палочки перенесли на ту же третью поверх 4-го кружка (причем 1-я палочка играла у нас роль вспомогательной), что опять потребовало семи отдельных перекладываний.
Итак, вообще, чтобы при таких условиях перенести колонну из n каких-нибудь кружков, расположенных вертикально в убывающем порядке, нужно сначала перенести колонну из (n-1) верхних кружков на одно из свободных мест, потом основание, т. е. n-й кружок, на другое свободное место и, наконец, на то же место опять всю колонну из (n-1) верхних кружков.
Обозначая число необходимых отдельных перенесений буквою П со значком, соответствующим числу кружков, имеем, следовательно,
![]()
Понижая значение n до единицы и делая подстановку, легко находим
![]()
Получаем, следовательно, сумму геометрической прогрессии, которая дает
![]()
Таким образом, в случае детской пирамиды из 8 кружков нужно сделать 28-1, или 255, отдельных перекладываний кружков.
Легенда. Если выше вместо 8 кружков возьмем 64 кружка, то получим задачу, связанную с древнеиндийской легендой. Легенда эта гласит, будто в городе Бенаресе, под куполом главного храма, в том месте, где находится середина Земли, бог Брама поставил вертикально на бронзовой площадке три алмазные палочки, каждая длиною в локоть и толщиною в корпус пчелы. При сотворении мира на одну из этих палочек были надеты 64 кружка из чистого золота с отверстиями посередине — так, что они образовали род усеченного конуса, так как диаметры их шли в возрастающем порядке, начиная сверху. Жрецы, сменяемые один другим, днем и ночью без устали трудятся над перенесением этой колонны кружков с первой палочки на третью, пользуясь второй как вспомогательной, причем они обязаны соблюдать уже указанные условия, т.е. 1) не переносить за один раз более одного кружка и 2) класть снятый кружок или на свободную в этот момент палочку, или накладывать его на кружок только большего диаметра. Когда, соблюдая все эти условия, жрецы перенесут все 64 кружка с первой палочки на третью, наступит конец мира…
Допустим, что перенос одного кружка продолжается всего одну секунду, тогда на перемещение пирамиды из восьми кружков потребуется 4 минуты с лишком. Что же касается переноса башни в 64 кружков, то на это понадобится
18 446 744 073 709 551 615 сек.
А это значит, ни более и ни менее, как пять с лишним миллиардов веков.
