Каждый, изучавший геометрию, знает, что сумма углов треугольника равна двум прямым углам. Но мало кому известно, что эта фундаментальная теорема может быть "доказана" с помощью простого лоскутка бумаги.
Мы ставим слово "доказана" в кавычках, потому что это не доказательство в строгом смысле слова, а скорее лишь наглядная демонстрация. Но все же этот остроумный прием очень любопытен и поучителен.
Вырезают из бумаги треугольник любой формы и перегибают его сначала по линии АВ (рис. 78) так, чтобы основание треугольника легло на себя. Затем, снова разогнув бумагу, перегибают треугольник по линии CD так, чтобы вершина А попала в точку В.
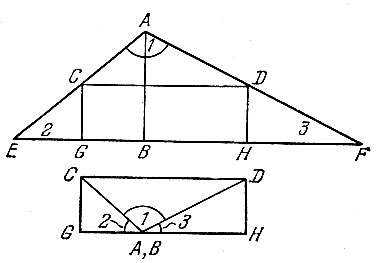
Рис. 78
Перегнув затем треугольник по линиям DH и CG так, чтобы точки Е и F попали в точку В, получим прямоугольник CGHD и наглядно убеждаемся, что все три угла треугольника (1, 2, 3) составляют в сумме два прямых.
Необычайная наглядность и простота этого приема позволяют познакомить даже детей, не изучавших геометрии, с одной из ее важнейших теорем. Для знающих же геометрию он представляет интересную задачу — объяснить, почему такое сгибание бумажного треугольника всегда дает желаемый результат. Объяснить это нетрудно, и мы не хотели бы лишить читателя удовольствия самому подыскать геометрическое обоснование этого своеобразного "доказательства".
