Построим прямоугольник со сторонами 11 см и 13 см. Рассечем его диагональю (рис. 114) и сдвинем затем полученные треугольники по их общей гипотез нузе в положение, показанное на рис. 115. Эта последняя фигура по виду состоит из квадрата VRXS со сторонами 12 см, т. е. площадью 122 см2 = 144 см2, и двух треугольников PQR и STU, каждый площадью 0,5 см2. Следовательно, площадь всей фигуры на рис. 115 равна 144 см2 + 2*0,5 см = 145 см2. Но как же это получилось, если площадь исходного прямоугольника равна только 13 см * 11 см = 143 см2?
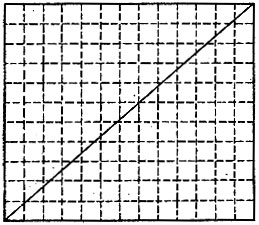
Рис. 114
Решение. Более подробное рассмотрение того, как диагональ пересекает клетки прямоугольника (рис. 114), показывает, что VRXS не есть квадрат. Это можно подтвердить и с помощью вычислений.
Из подобных треугольников PQR и TQX получаем PR:QR = TX:QX и PR = TX*QR/QX = 11*1/13 = 11/13. Значит, стороны прямоугольника VRXS равны 12 см и 11 11/13 см, а площадь равна 12 см * 11 11/13 = 142 2/13 см2. Площадь треугольника STU равна площади треугольника PQR и равна 1/2*1 см * 11/13 см = 11/26 см2. Таким образом, площадь фигуры равняется 142 2/13 см2 + 2*11/26 см2 =143 см2.
