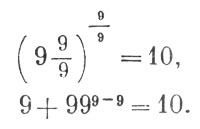101. Можно выполнить требуемую работу, раскрыв только три звена. Для этого надо освободить звенья одного обрывка и соединить ими концы остальных четырех обрывков.
102. Чтобы решить эту задачу, нужно прежде всего припомнить из естественной истории, сколько ног у жуков и сколько у пауков: у жука 6 ног, у паука — 8.
Зная это, предположим, что в коробке были одни только жуки, числом 8 штук. Тогда всех ног было бы 6X8 = 48, на 6 меньше, чем указано в задаче. Заменим теперь одного жука пауком. От этого число ног увеличится на 2, потому что у паука не 6 ног, а 8.
Ясно, что если мы сделаем три такие замены, мы доведем общее число ног в коробке до требуемых 54. Но тогда из 8 жуков останется только 5, остальные будут пауки.
Итак, в коробке было 5 жуков и 3 паука.
Проверим: у 5 жуков 30 ног, у 3 пауков 24 ноги, а всего 30 + 24 = 54, как и требует условие задачи.
Можно решить задачу и иначе. А именно: можно предположить, что в коробке были только пауки, 8 штук. Тогда всех ног оказалось бы 8 X 8 = 64, — на 10 больше, чем указано в условии. Заменив одного паука жуком, мы уменьшим число ног на 2. Нужно сделать 5 таких замен, чтобы свести число ног к требуемым 54. Иначе говоря, из 8 пауков надо оставить только 3, а остальных заменить жуками.
103. Если бы вместо плаща, шляпы и галош куплено было только две пары галош, то пришлось бы заплатить не 20 руб., а на столько меньше, на сколько галоши дешевле плаща с шляпой, т. е. на 16 руб. Мы узнаем, следовательно, что две пары галош стоят 20-16 = 4 руб., отсюда стоимость одной пары — 2 руб.
Теперь стало известно, что плащ и шляпа вместе стоят 20-2 = 18 руб., причем плащ дороже шляпы на 9 руб. Рассуждаем, как прежде: вместо плаща с шляпой, купим две шляпы. Мы заплатим не 18 руб., а меньше на 9 руб. Значит, две шляпы стоят 18-9 = 9 руб., откуда стоимость одной шляпы — 4 руб. 50 коп.
Итак, вот стоимость вещей: галоши — 2 руб., шляпа — 4 руб. 50 коп., плащ — 13 руб. 50 коп.
104. Продавец имел в виду корзину с 29 яйцами. Куриные яйца были в корзинах с обозначениями 23, 12 и 5 утиные — в корзинах с числами 14 и 6.
Проверим. Всего куриных яиц оставалось:
23 + 12 + 5 = 40.
Утиных
14 + 6 = 20.
Куриных вдвое больше, чем утиных, как и требует условие задачи.
105. В этой задаче нечего объяснять: самолет совершает перелет в обоих направлениях в одинаковое время, потому что 80 мин. = 1 ч. 20 м.
Задача рассчитана на невнимательного читателя, который может подумать, что между 1 ч. 20 м. и 80 мин. есть разница. Как ни странно, но людей, попадающихся на этот крючок, оказывается немало, притом среди привыкших делать расчеты их больше, чем среди малоопытных вычислителей. Причина кроется в привычке к десятичной системе мер и денежных единиц. Видя обозначение: 1 ч. 20 м. и рядом с ним 80 мин., мы невольно оцениваем различие между ними, как разницу между 1 р. 20 к. и 80 коп. На эту психологическую ошибку и рассчитана задача.
106. Разгадка недоумения в том, что один из отцов приходился другому сыном. Всех было не четверо, а трое: дед, сын и внук. Дед дал сыну 150 руб., а тот передал из них 100 руб. внуку (т. е. своему сыну), увеличив собственные капиталы, следовательно, всего на 50 руб.
107. Первую шашку можно поместить на любое из 64 полей доски, т. е. 64 способами. После того как первая поставлена, вторую шашку можно поместить на какое-либо из прочих 63 полей. Значит к каждому из 64 положений первой шашки можно присоединить 63 положения второй шашки. Отсюда общее число различных положений двух шашек на доске
64 X 63 = 4032.
108. Наименьшее целое число, какое можно написать двумя цифрами, не 10, как думают, вероятно, иные читатели, а единица, выраженная таким образом:
1/1, 2/2, 3/3, 4/4 и т. д. до 9/9.
Знакомые с алгеброй прибавят к этим выражениям еще и ряд других обозначений:
1°, 2°, 3°, 4° и т. д. до 9°,
Потому, что всякое число в нулевой степени равно единице*.
* (Но неправильны были бы решения 0/0 или 0°; эти выражения вообще не имеют смысла.)
109. Надо представить единицу как сумму двух дробей
148/296 +35/70 = 1.
Знающие алгебру могут дать еще и другие ответы:
1234567890; 2345679-8-1
И т. п., так как число в нулевой степени равно единице.
110. Два способа таковы:
9 99/99 = 10,
99/9 - 9/9 = 10.
Кто знает алгебру, тот может прибавить еще несколько решений, например: