46. 888 + 88 + 8 + 8 + 8 = 1000.
Имеются и другие решения.
47. Вот два решения:
22 + 2 = 24; 33 - 3 = 24.
48. Приводим три решения:
6 x 6 - 6 = 30; 33 + 3 = 30; 33 - 3 = 30.
49. Недостающие цифры восстанавливаются постепенно, если применить следующий ход рассуждений.
Для удобства пронумеруем строки:
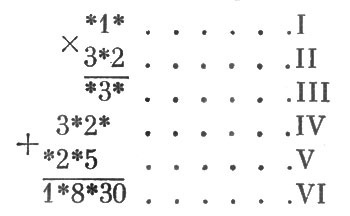
Легко сообразить, что последняя звездочка в III строке цифр есть 0: это ясно из того, что 0 стоит в конце VI строки.
Теперь определяется значение последней звездочки I строки: это — цифра, которая от умножения на 2 дает число, оканчивающееся нулем, а от умножения на 3 — число, оканчивающееся 5 (V ряд). Цифра такая только одна — 5.
Ясно далее, что в конце IV строки стоит цифра 0. (Сравните цифры, стоящие на втором с конца месте в III и VI строках!)
Нетрудно догадаться, что скрывается под звездочкой II строки: 8, потому что только 8 при умножении на число 15 дает результат, оканчивающийся 20 (IV строка).
Наконец, становится ясным значение первой звездочки строки I: это цифра 4, потому что только 4, умноженное на 8, дает результат, начинающийся на 3 (строка IV).
Узнать остальные неизвестные цифры теперь не составляет никакой трудности: достаточно перемножить числа первых двух строк, уже вполне определившиеся.
В конечном итоге получаем такой пример умножения:
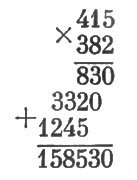
50. Подобным сейчас примененному ходом рассуждений раскрываем значение звездочек и в этом случае.
Получаем:
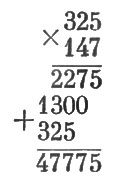
51. Вот искомый случай деления:

