§ 3. Признаки равенства треугольников → номер 21
1)
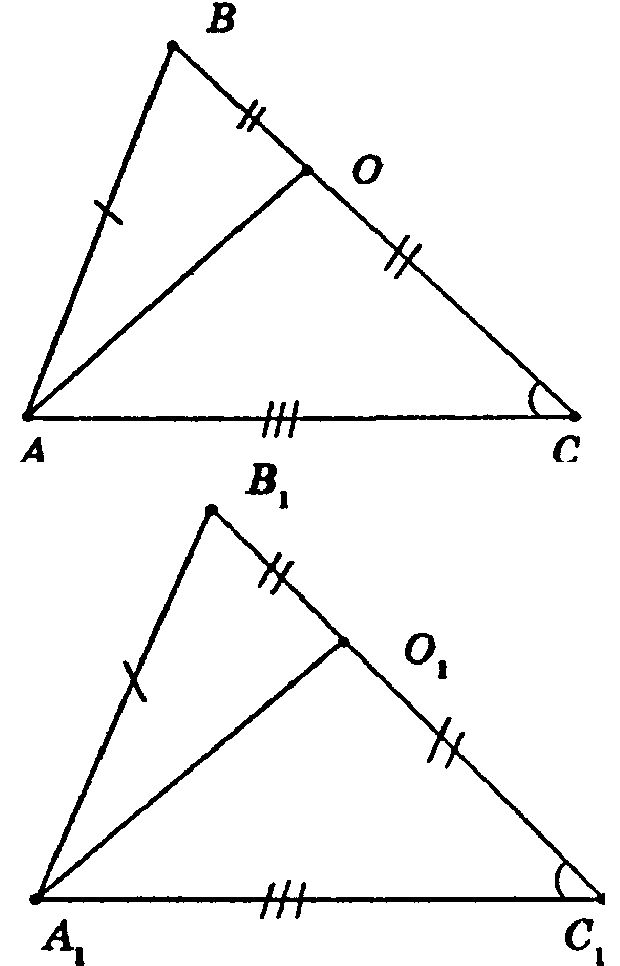
∠С = ∠C1, ∠А = ∠А1, ∠В = ∠В1
ВО = ОС = В1О1 = О1С1, т. к. АО и А1О1 — медианы, и ВС = В1С1.
В ΔАОС и ΔА1О1С1: АС = А1С1, ОС = О1С1, ∠С = ∠С1. Таким образом, ΔАОС = ΔА1О1С1 по 1-му признаку, откуда АО = А1О1. 2)
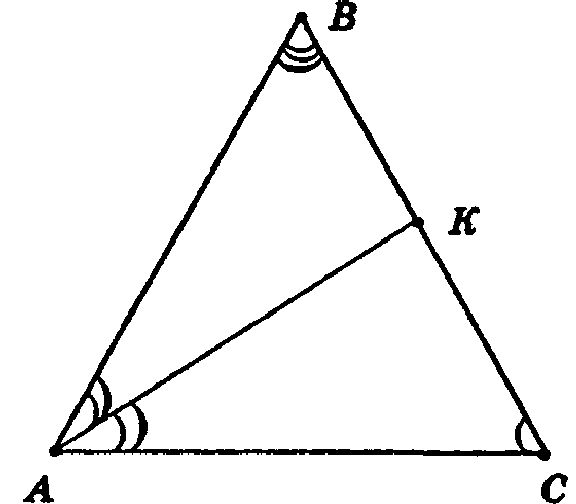
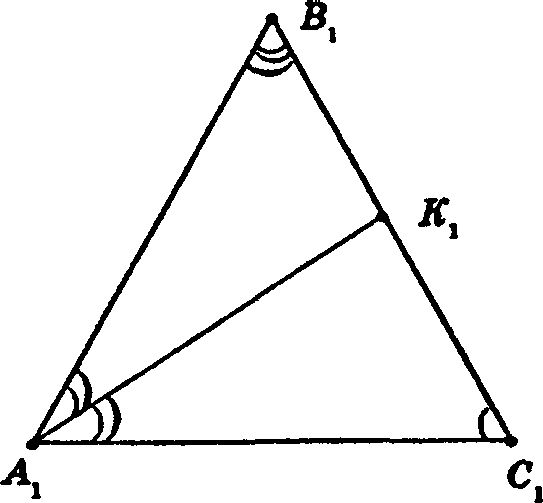
Т. к. ΔАВС = ΔA1B1C1, то: AC = А1С1, ∠A = ∠А1, ∠С = ∠С1.
∠BAK = ∠KAC = ∠B1A1K1 = ∠K1A1C1, т. к. AK и A1K1 — биссектрисы равных углов.
В ΔAKC и ΔA1K1C1: АС = А1С1, ∠С = ∠С1, ∠KAC = ∠K1A1C1. Таким образом, ΔAKC = ΔA1K1C1 по 2-му признаку равенства треугольников.
Откуда AK = A1K1.
Т. к. ΔАВС = ΔA1B1C1, то: AC = А1С1, ∠A = ∠А1, ∠С = ∠С1.
∠BAK = ∠KAC = ∠B1A1K1 = ∠K1A1C1, т. к. AK и A1K1 — биссектрисы равных углов.
В ΔAKC и ΔA1K1C1: АС = А1С1, ∠С = ∠С1, ∠KAC = ∠K1A1C1. Таким образом, ΔAKC = ΔA1K1C1 по 2-му признаку равенства треугольников.
Откуда AK = A1K1.
