Дополнительные задачи к главе I Параллельность прямых и плоскостей. → номер 100
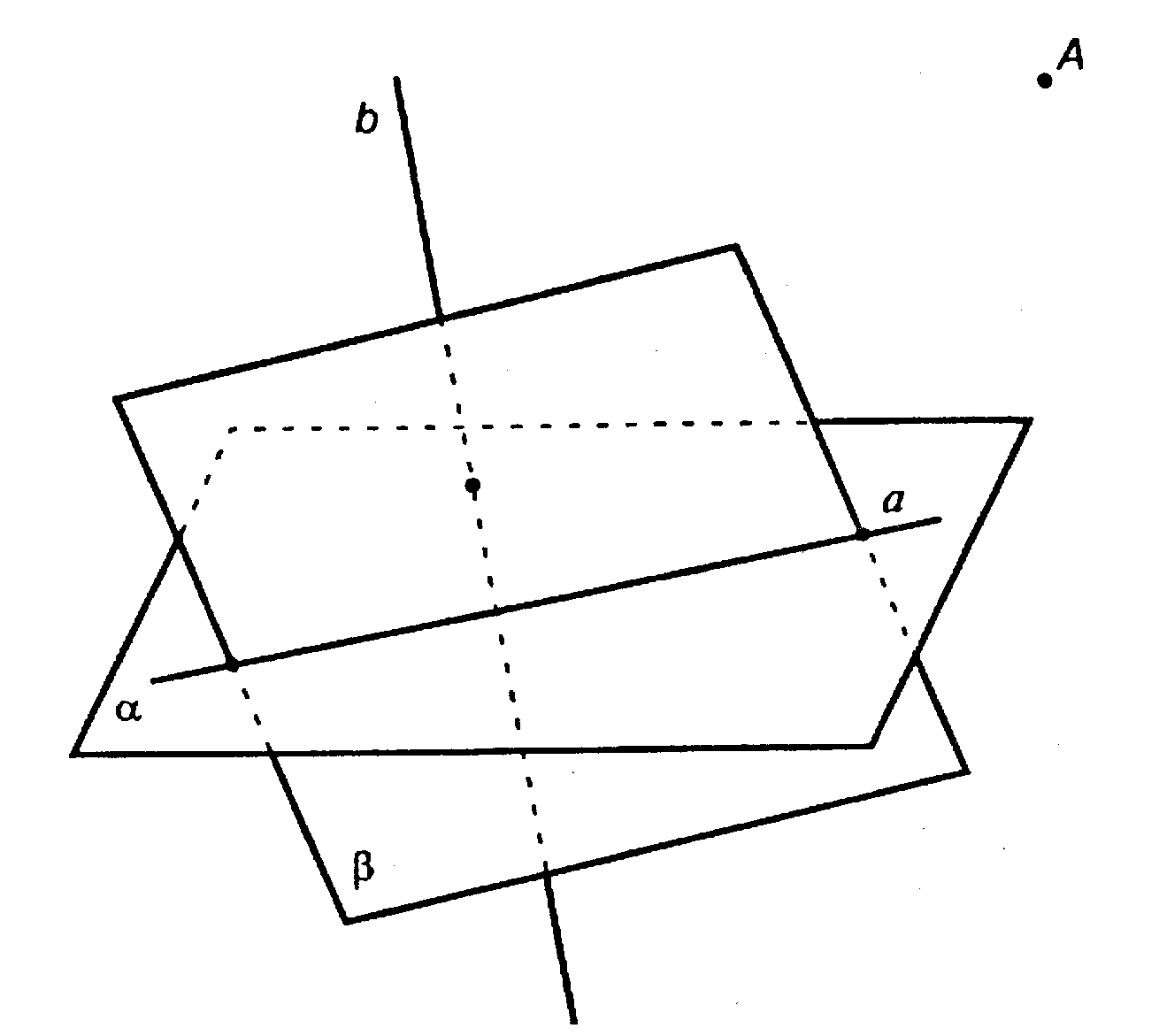
А и b — скрещиваются, а ⊂ α.
По теореме о скрещивающихся прямых (п. 7, теорема вторая), через прямую а можно провести единственную плоскость β || b.
Докажем, что через т. А можно провести плоскость γ, такую что γ || β.
Через точку А провести плоскость, параллельную данной плоскости β не проходящей через т. А.
Проводим в пл. β через некоторую т. В две произвольные прямые BD и ВС. Строим две вспомогательные плоскости: плоскость М — через т. А и прямую ВС и плоскость N — через т. А и прямую BD. Искомая плоскость, параллельная пл. β, должна пересечь пл. М по прямой, параллельной ВС, а плоскость N — по прямой, параллельной BD (п. 11, 1о). Отсюда способ построения пл. γ: через т. А проводим
В пл. М прямую АС1 || BC, а в пл. N прямую AD1 || BD. Через прямые АС1 и AD1 проводим пл. γ. γ — искомая, так как стороны ∠D1AC1, расположенного в пл. γ, параллельны сторонам ∠DBC, расположенного в пл. β. Значит, γ || β.
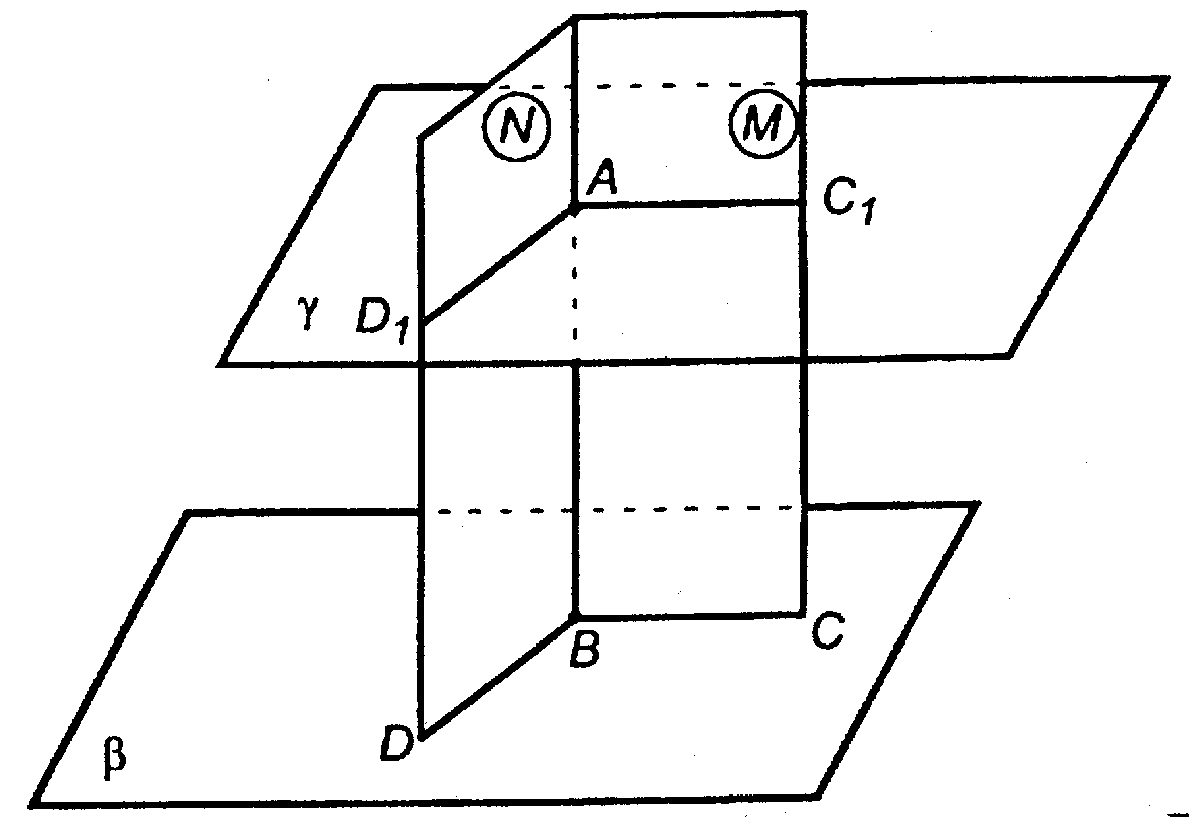
Так как в пл. М через т. А можно провести лишь одну прямую, параллельную ВС, а в плоскости N через т. А можно провести лишь одну прямую, параллельную BD, то задача имеет единственное решение.
Следовательно, через каждую точку пространства можно провести единственную плоскость, параллельную данной плоскости; γ — единственная плоскость.
Если же окажется, что т. А ∈ β, то это и будет тот случай, когда через т. А и прямую а проходит пл. β, параллельная прямой b.
