Глава II Перпендикулярность прямых и плоскостей. §1 Перпендикулярность прямой и плоскости → номер 128
Дано:
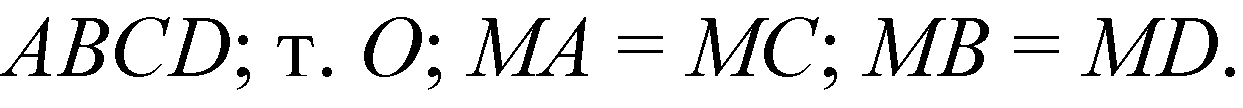
Решение:
Точка М равноудалена от А и С, B и D. Значит, она лежит на серединном перпендикуляре к АС и BD. То есть ОМ ⊥ АС, ОМ ⊥ BD. По признаку перпендикулярности прямой и плоскости ОМ ⊥ пл. АВС.
Что и требовалось доказать.
