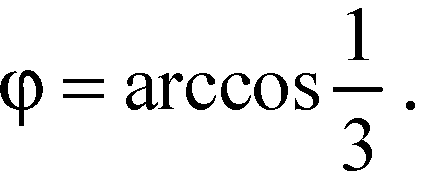Глава II Перпендикулярность прямых и плоскостей. §3 Двугранный угол. Перпендикулярность плоскостей. → номер 175
* В задачах этого параграфа двугранный угол с ребром АВ, на разных гранях которого отмечены точки С и D, для краткости будем называть так: двугранный угол CABD.
Решение:
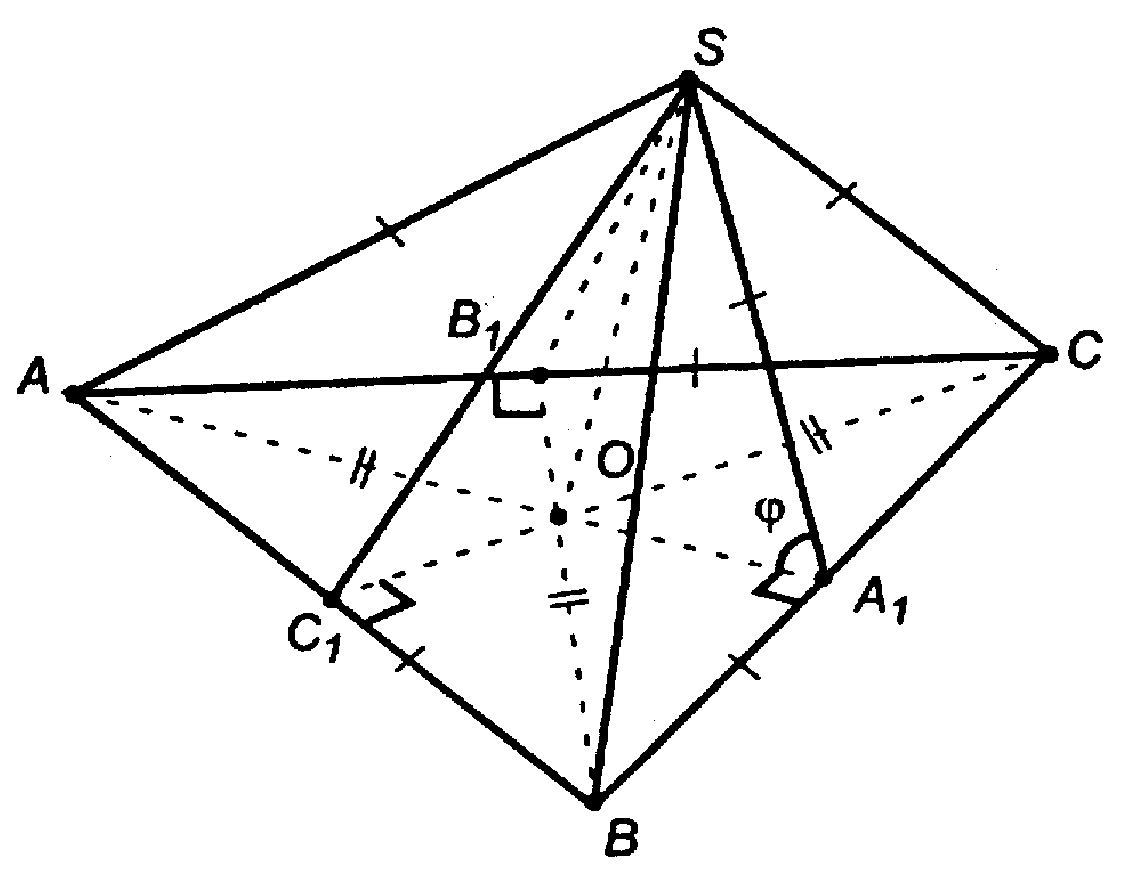
Построим SO ⊥ пл. АВС.
SA, SB, SC — наклонные, а равные наклонные имеют равные проекции, поэтому АО=ВО = СО; поэтому в пл. АВС АО = R, R — радиус описанной окружности.
ΔАВС — правильный; продолжим АО, СО и ВО до пересечения их со сторонами треугольника.
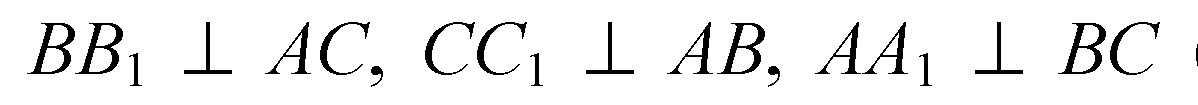
(из свойств правильного треугольника).
Соединим точки S и В, А1 и S, С1 и S.
∠SB1O — линейный угол двугранного угла SAСВ. ∠SC1O — линейный угол двугранного угла SABC.
∠SA1O — линейный угол двугранного угла SBCA (по определению).
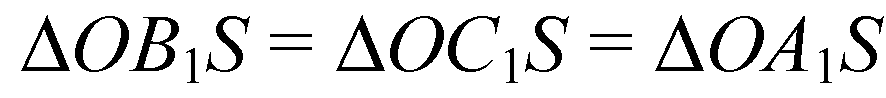
— по двум катетам
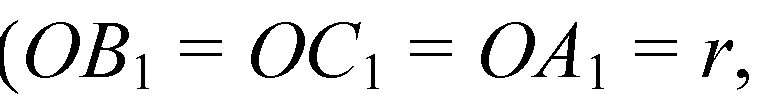
R — радиус вписанной окружности в ΔАВС, SO — общий катет),
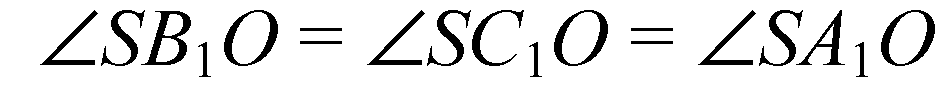
(из равенства треугольников).
Раз все ребра тетраэдра равны, то доказанное выше справедливо и для всех двугранных углов.
Поэтому все двугранные углы равны.
Отыщем один из линейных углов двугранного угла, например, ∠SA1O двугранного угла SBCA.
Пусть а — ребро тетраэдра, то имеем
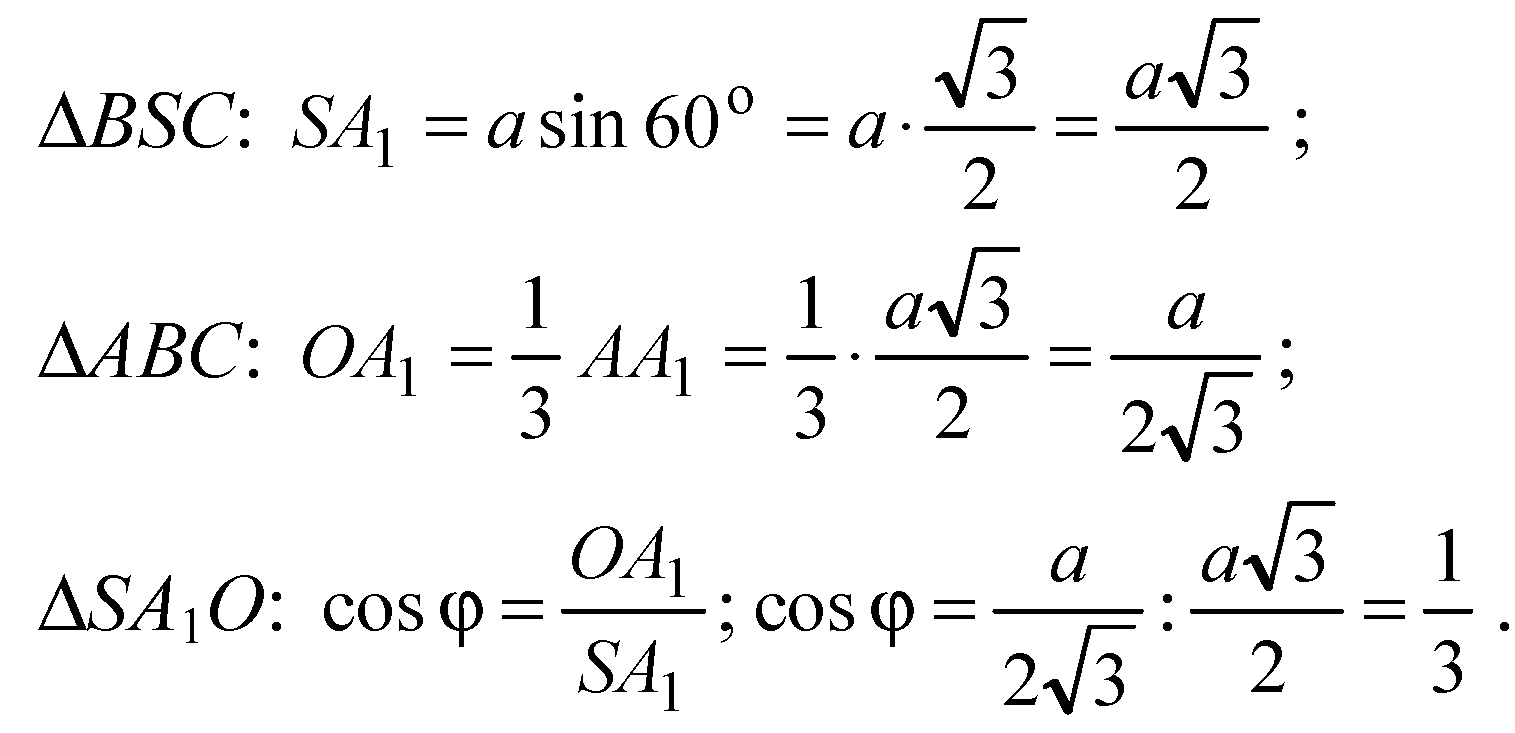
φ — острый угол.
Отсюда:
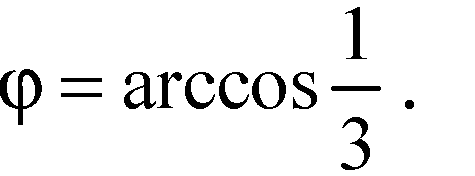
Ответ: